A symmetric chain decomposition of L(5, n)
A symmetric chain decomposition of L(5, n)
Xiangdong Wen
Wolfram Research
Wolfram Research
Young’s lattice L(m,n)
Young’s lattice L(m,n)
Young Diagram
Young Diagram
In[]:=
IntegerPartitions[5]
Out[]=
{{5},{4,1},{3,2},{3,1,1},{2,2,1},{2,1,1,1},{1,1,1,1,1}}
In[]:=
Options[youngDiagram]={ItemSize->20};youngDiagram[a_List,OptionsPattern[]]:=If[Length[a]>0&&a[[1]]>0,Graphics[{EdgeForm[Black],FaceForm[Yellow],Table[Table[Rectangle[{j,-i},{(j+1),(-i-1)}],{j,1,a[[i]]}],{i,1,Length[a]}]},ImageSize->OptionValue[ItemSize]*a[[1]]],Graphics[{EdgeForm[Black],FaceForm[White],Disk[],Line[{{-1,-1},{1,1}}]},ImageSize->OptionValue[ItemSize]]];
In[]:=
Map[youngDiagram,%1]
Out[]=
Young’s lattice
Young’s lattice
In[]:=
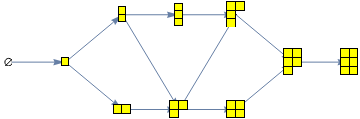
expand[a_]:=Table[{i,Sequence@@a},{i,0,a[[1]]}];L[1,n_]:=Table[{i},{i,0,n}];L[m_,n_]:=Sort[Join@@Map[expand,L[m-1,n]]];edgesR[sa_]:=Module[{r,im,t=1,s},s=Map[First,sa];im=IdentityMatrix[Length[s[[1]]]];r=Table[Null,Length[s]*Length[s[[1]]]];Do[r[[t++]]=If[MemberQ[s,e+i]&&Union[((e+i)/.sa)-(e/.sa),{0}]=={0,1},{e,e+i},Nothing],{e,s},{i,im}];r];edges[s_]:=edgesR[Map[#->#&,s]];coords[a_,p_]:=Module[{l},l=Length[a];Table[{i*50-25*l,p*30},{i,1,l}]];Options[youngLattice]={ItemSize->10,GraphLayout->Left};data[m_,n_]:=Module[{v,e,p,v2i,i2v},p=If[n==0,Table[IntegerPartitions[i],{i,0,m}],Table[Select[IntegerPartitions[i],Length[#]<=m&&(Length[#]==0||First[#]<=n)&],{i,0,m*n}]]/.{}->{0};v=Map[PadRight[#,m]&,Apply[Join,p]];e=edges[v];v2i=MapIndexed[#1->First[#2]&,v];i2v=MapIndexed[First[#2]->#1&,v];{p,v,e,v2i,i2v}];youngLattice[m_,n_Integer:0,OptionsPattern[]]:=Module[{v,e,vl,c,p,vc,v2i,i2v},{p,v,e,v2i,i2v}=data[m,n];c=Apply[Join,MapIndexed[coords[#1,First[#2]]&,p]];vl=Table[Evaluate[t/.v2i]->Placed[youngDiagram[t/.{0->Nothing},ItemSize->OptionValue[ItemSize]],Center],{t,v}];vc=Switch[OptionValue[GraphLayout],Up,Map[{#[[1]],-#[[2]]}&,c],Down,Map[{#[[1]],#[[2]]}&,c],Left,Map[{#[[2]],#[[1]]}&,c],Right,Map[{-#[[2]],#[[1]]}&,c]];Graph[Map[#[[1]]->#[[2]]&,e]/.v2i,VertexLabels->vl,VertexCoordinates->vc]];
In[]:=
youngLattice[5,GraphLayout->Up]
Out[]=
In[]:=
youngLattice[2,3]
Out[]=
In[]:=
youngLattice[3,2]
Out[]=
Symetric Chain Decomposition
Symetric Chain Decomposition
Chain < < < ⋯ < , ∈ L(m,n)
saturated: rank() - rank = 1, s=2,3,⋯,t
symmetric: rank() + rand() = m n
SCD: Partition a poset into disjoint symmetric chains.
Poset with a SCD is called symmeric chain order.
v
1
v
2
v
3
v
t
v
i
saturated: rank(
v
s
()
v
s-1
symmetric: rank(
v
1
v
t
SCD: Partition a poset into disjoint symmetric chains.
Poset with a SCD is called symmeric chain order.
In[]:=
rank[v_]:=Total[v];Options[scdL]={ItemSize->10,GraphLayout->Left};scdL[m_,n_,OptionsPattern[]]:=Module[{v,e,vl,c,p,vc,v2i,i2v,edges,from,to,rest,flow={},singles,g},{p,v,e,v2i,i2v}=data[m,n];edges=Map[#[[1]]->#[[2]]&,e]/.v2i;c=Apply[Join,MapIndexed[coords[#1,First[#2]]&,p]];vl=Table[Evaluate[t/.v2i]->Placed[youngDiagram[t/.{0->Nothing},ItemSize->OptionValue[ItemSize]],Center],{t,v}];vc=Switch[OptionValue[GraphLayout],Up,Map[{#[[1]],-#[[2]]}&,c],Down,Map[{#[[1]],#[[2]]}&,c],Left,Map[{#[[2]],#[[1]]}&,c],Right,Map[{-#[[2]],#[[1]]}&,c]];Do[from=Select[v,Total[#]==Floor[(mn/2)]-i&]/.v2i;to=Select[v,Total[#]==Ceiling[(mn/2)]+i&]/.v2i;rest=Select[Map[{#[[1]],#[[2]]}&,edges],MemberQ[Map[First,flow],#[[1]]]==False&];g=Sort[Map[#[[1]]->#[[2]]&,Join[flow,rest]]];flow=Join[flow,Select[Map[First,Select[ArrayRules@FindMaximumFlow[g,from,to,"OptimumFlowData",VertexCapacity->Table[1,{j,1Length[v]}]]["FlowMatrix"],#[[2]]==1&]],Length[Intersection[#,Join[from,to]]]>0&]],{i,0,Floor[(mn/2)]}];singles=Complement[Range[Length[v]],Apply[Union,flow]];Graph[Join[Map[#[[1]]->#[[2]]&,flow],Map[#->#&,singles]],VertexCoordinates->MapIndexed[First[#2]->#1&,vc],VertexLabels->vl]]
In[]:=
scdL[2,3]
Out[]=
O’hara subposets L(m,n,s) and L(m,n,s,d)
O’hara subposets L(m,n,s) and L(m,n,s,d)
spread, degree
spread, degree
https://sites.math.rutgers.edu/~zeilberg/mamarim/mamarimPDF/ohara.pdfspread(a) := max{-, 2 ⩽i ⩽ m+1}, =0;=nM(a):={2⩽i⩽m+1;-=spread(a)}M(a) = ⋃, are maximally connected intervalsdegree(a):= []
a
i
a
i-2
a
0
a
m+1
a
i
a
i-2
D
j
D
j
∑
j
+1
D
j
2
In[]:=
spread[a_,n_]:=Max[Join[Rest[a],{n}]-Join[{0},Most[a]]]
In[]:=
degree[a_,n_]:=Total[Map[Floor[(Total[#]+1)/2]&,Split[BinCounts[Flatten@Position[Join[Rest[a],{n}]-Join[{0},Most[a]],spread[a,n]],1]]]]
L(m,n,s), L(m,n,s,d), U(m,n,s)
L(m,n,s), L(m,n,s,d), U(m,n,s)
L(m,n,s) := {v ∈ L(m,n), spread[v]=s}
L(m,n,s,d):= {v ∈ L(m,n), spread[v]=s, degree[v]=d }
U(m,n,s) := {v ∈ L(m,n), spread[v] ⩽ s}
L(m,n,s,d):= {v ∈ L(m,n), spread[v]=s, degree[v]=d }
U(m,n,s) := {v ∈ L(m,n), spread[v] ⩽ s}
Visualization Tools
Visualization Tools
Tools
Tools
Examples
Examples
Are all L(5,n,s,1) symmetric chain orders?
Are all L(5,n,s,1) symmetric chain orders?
It is still an open problem.
Are all L(5,n,s,2) symmetric chain orders?
Are all L(5,n,s,2) symmetric chain orders?
Yes.
Are all L(5,n,s,3) symmetric chain orders?
Are all L(5,n,s,3) symmetric chain orders?
Yes.
SCDL5n(n)
SCDL5n(n)
Visualize Chains of L(5,n)
Visualize Chains of L(5,n)
L(6,n)
L(6,n)