In[]:=
fsfmachines//Length
Out[]=
6932
fsfmachines
In[]:=
Values[fsfmachines]
Out[]=
In[]:=
Union[%]
Out[]=
In[]:=
Cases[%283,_Times]
Out[]=
{2n,4n,6n,8n,10n,12n,14n,16n,18n,20n,24n,2,3,4,5,6,8,9,10}
2
n
2
n
2
n
2
n
2
n
2
n
2
n
2
n
In[]:=
Take[%283,15]
Out[]=
{1,3,5,7,9,11,13,15,17,19,21,25,2n,4n,6n}
In[]:=
CountsHead/@
Out[]=
Integer12,Times19,Power1,Failed851,LR1924,Per27,PerDiff690
In[]:=
Length
Out[]=
3524
In[]:=
Select[Normal[fsfmachines],Last[#]==11&]
Out[]=
{{1,11,9,11,11,11,11,11,11,11}11,{1,11,7,11,11,11,11,11,11,11}11,{1,5,11,11,11,11,11,11,11,11}11,{1,5,7,11,11,11,11,11,11,11}11,{1,9,7,11,11,11,11,11,11,11}11,{1,3,11,11,11,11,11,11,11,11}11,{1,7,11,11,11,11,11,11,11,11}11,{1,11,5,11,11,11,11,11,11,11}11,{1,9,11,11,11,11,11,11,11,11}11,{1,3,7,11,11,11,11,11,11,11}11,{11,3,9,11,11,11,11,11,11,11}11,{7,5,11,11,11,11,11,11,11,11}11,{11,5,7,11,11,11,11,11,11,11}11,{5,3,11,11,11,11,11,11,11,11}11,{9,11,9,11,11,11,11,11,11,11}11,{9,11,7,11,11,11,11,11,11,11}11,{11,9,7,11,11,11,11,11,11,11}11,{9,3,11,11,11,11,11,11,11,11}11,{3,9,11,11,11,11,11,11,11,11}11,{11,3,11,11,11,11,11,11,11,11}11,{11,3,5,11,11,11,11,11,11,11}11,{11,7,9,11,11,11,11,11,11,11}11,{11,5,9,11,11,11,11,11,11,11}11,{11,11,9,11,11,11,11,11,11,11}11,{3,11,11,11,11,11,11,11,11,11}11,{9,11,11,11,11,11,11,11,11,11}11,{11,7,11,11,11,11,11,11,11,11}11,{3,3,11,11,11,11,11,11,11,11}11,{5,7,11,11,11,11,11,11,11,11}11,{3,7,11,11,11,11,11,11,11,11}11,{3,11,7,11,11,11,11,11,11,11}11,{3,11,5,11,11,11,11,11,11,11}11,{11,9,11,11,11,11,11,11,11,11}11,{9,7,11,11,11,11,11,11,11,11}11,{5,9,11,11,11,11,11,11,11,11}11,{9,5,11,11,11,11,11,11,11,11}11,{9,9,11,11,11,11,11,11,11,11}11,{11,7,5,11,11,11,11,11,11,11}11,{7,11,5,11,11,11,11,11,11,11}11,{5,11,11,11,11,11,11,11,11,11}11,{11,5,5,11,11,11,11,11,11,11}11,{5,11,5,11,11,11,11,11,11,11}11,{7,5,7,11,11,11,11,11,11,11}11,{5,11,9,11,11,11,11,11,11,11}11,{5,11,7,11,11,11,11,11,11,11}11,{3,9,7,11,11,11,11,11,11,11}11,{7,11,9,11,11,11,11,11,11,11}11,{7,9,11,11,11,11,11,11,11,11}11,{3,5,11,11,11,11,11,11,11,11}11,{7,7,11,11,11,11,11,11,11,11}11,{5,7,9,11,11,11,11,11,11,11}11,{3,11,9,11,11,11,11,11,11,11}11,{7,11,7,11,11,11,11,11,11,11}11,{11,5,11,11,11,11,11,11,11,11}11,{1,11,11,11,11,11,11,11,11,11}11,{11,3,7,11,11,11,11,11,11,11}11,{7,3,11,11,11,11,11,11,11,11}11,{7,7,9,11,11,11,11,11,11,11}11,{7,7,7,11,11,11,11,11,11,11}11,{5,3,7,11,11,11,11,11,11,11}11,{7,11,11,11,11,11,11,11,11,11}11,{11,9,9,11,11,11,11,11,11,11}11,{7,3,5,11,11,11,11,11,11,11}11,{5,9,9,11,11,11,11,11,11,11}11,{5,9,7,11,11,11,11,11,11,11}11}
In[]:=
Take[tnew3,3]
Out[]=
{{{{0,2,0,4,4,6,0,8,8,10,8,12,12,14,0,16,16,18,16,20,20,22,16,24,24,26,24,28,28,30,0,32},{3,5,7,9,11}},20736},{{{0,2,0,4,4,6,0,8,8,10,8,12,12,14,0,16,16,18,16,20,20,22,16,24,24,26,24,28,28,30,0,32},{3,5,7,9,11}},20737},{{{0,2,0,4,4,6,0,8,8,10,8,12,12,14,0,16,16,18,16,20,20,22,16,24,24,26,24,28,28,30,0,32},{3,5,7,9,11}},20738}}
In[]:=
Select[fsfmachines,Head[Last[#]]===Power&]
Out[]=
{{9,17,27,39,53,69,87,107,129,153},{11,19,29,41,55,71,89,109,131,155},{17,27,39,53,69,87,107,129,153,179},{3,7,13,21,31,43,57,73,91,111},{5,11,19,29,41,55,71,89,109,131},{13,23,35,49,65,83,103,125,149,175},{7,15,25,37,51,67,85,105,127,151},{1,5,11,19,29,41,55,71,89,109},{1,3,7,13,21,31,43,57,73,91},{1,3,11,21,33,47,63,81,101,123},{1,5,9,15,23,33,45,59,75,93},{1,3,9,17,27,39,53,69,87,107},{5,13,23,35,49,65,83,103,125,149},{11,21,33,47,63,81,101,123,147,173},{9,11,19,31,45,61,79,99,121,145},{3,9,17,27,39,53,69,87,107,129},{15,25,37,51,67,85,105,127,151,177},{1,11,19,29,41,55,71,89,109,131},{1,13,25,39,55,73,93,115,139,165},{1,7,13,21,31,43,57,73,91,111},{1,9,15,23,33,45,59,75,93,113},{1,9,17,27,39,53,69,87,107,129},{1,11,21,33,47,63,81,101,123,147},{1,13,21,31,43,57,73,91,111,133},{1,5,13,23,35,49,65,83,103,125},{1,11,17,25,35,47,61,77,95,115},{1,7,9,11,19,29,41,55,71,89},{3,11,21,33,47,63,81,101,123,147},{5,9,15,23,33,45,59,75,93,113},{7,13,21,31,43,57,73,91,111,133},{7,15,27,41,57,75,95,117,141,167},{9,15,23,33,45,59,75,93,113,135},{1,3,11,17,25,35,47,61,77,95},{3,5,13,23,35,49,65,83,103,125},{5,7,11,19,29,41,55,71,89,109},{1,7,15,25,37,51,67,85,105,127},{1,7,17,29,43,59,77,97,119,143},{1,11,23,37,53,71,91,113,137,163}}
2
n
2
n
2
n
2
n
2
n
2
n
2
n
2
n
2
n
2
n
2
n
2
n
2
n
2
n
2
n
2
n
2
n
2
n
2
n
2
n
2
n
2
n
2
n
2
n
2
n
2
n
2
n
2
n
2
n
2
n
2
n
2
n
2
n
2
n
2
n
2
n
2
n
2
n
In[]:=
revfind[list_]:=Cases[tnew3,{{_,Take[list,5]},m_}->m]
In[]:=
revfind[{7,5,11,11,11,11,11,11,11,11}]
Out[]=
{1026185,1026187,1067657,1067659,1088393,1088395,1092597,1092599,1109129,1109131,1129865,1129867,1134069,1134071,1150601,1150603,1192073,1192075,1233545,1233547,1528053,1528055,1569477,1569479,1569525,1569527,1590261,1590263,1590789,1590791,1610997,1610999,1631733,1631735,1652469,1652471,1673205,1673207,1693933,1693935,1693941,1693943,1693983,1714677,1714679,1735405,1735407,1735413,1735415,1735455,2017986,2018274,2059458,2059746,2100930,2101218,2142402,2142690,2163138,2163426,2172867,2173155,2183874,2184162,2204610,2204898,2214339,2214627,2225346,2225634,2525379,2525667,2553027,2553315,2566851,2567139,2587587,2587875,2601123,2607747,2608035,2608323,2608611,2629059,2629347,2642595,2649219,2649507,2649795,2650083,2656715,2657003,2670531,2670819,2691267,2691555,2712003,2712291,2732739,2733027}
In[]:=
revfind2[list_]:=With[{u=revfind[list]},Select[u,WorstCases[OneSidedTuringMachineFunction[{#,3,2},{1,2^Length[list]},10^7,"Steps"]]===list&]]
In[]:=
revfind2[{7,5,11,11,11,11,11,11,11,11}]
Out[]=
{1026185,1026187,1067657,1067659,1088393,1088395,1092597,1092599,1109129,1109131,1129865,1129867,1134069,1134071,1150601,1150603,1192073,1192075,1233545,1233547,1528053,1528055,1569477,1569479,1569525,1569527,1590261,1590263,1590789,1590791,1610997,1610999,1631733,1631735,1652469,1652471,1673205,1673207,1693933,1693935,1693941,1693943,1693983,1714677,1714679,1735405,1735407,1735413,1735415,1735455,2017986,2018274,2059458,2059746,2100930,2101218,2142402,2142690,2163138,2163426,2172867,2173155,2183874,2184162,2204610,2204898,2214339,2214627,2225346,2225634,2525379,2525667,2553027,2553315,2566851,2567139,2587587,2587875,2601123,2607747,2608035,2608323,2608611,2629059,2629347,2642595,2649219,2649507,2649795,2650083,2656715,2657003,2670531,2670819,2691267,2691555,2712003,2712291,2732739,2733027}
In[]:=
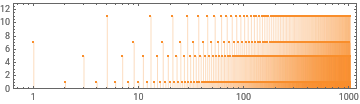
ListPlot[OneSidedTuringMachineFunction[{1026185,3,2},{1,2^10},10^7,"Steps"],Filling->Axis,PlotStyle->StandardOrange,AspectRatio->1/4,Frame->True,ScalingFunctions->{"Log",Identity},PlotRange->{0,13}]
Out[]=
FrameTicks
In[]:=
rtplot[m_,max_,rtmax_:10^7,opts___]:=With[{u=OneSidedTuringMachineFunction[m,{1,2^max},rtmax,"Steps"]},{v=WorstCases[u]},Show[{ListStepPlot[Transpose[{PowerRange[1,2^Length[v]-1,2],v}],opts,Filling->Axis,FrameTicks->{{Automatic,Automatic},{PowerRange[1,2^max,2],Automatic}},PlotStyle->Opacity[.3,Gray],AspectRatio->1/4,Frame->True,ScalingFunctions->{"Log",Identity}],ListPlot[u,Filling->Axis,PlotStyle->StandardOrange,AspectRatio->1/4,Frame->True,ScalingFunctions->{"Log",Identity}]}]]
NONLINEAR: