Wolfram Cloud Page

In[]:=

OneSidedTuringMachineEvolution[{1955095,3,2},42,30][[-1,-1]]

Out[]=

{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,1,0,1,1,1,0}

Length[#]-FirstPosition[#,1][[1]]+4

In[]:=

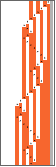
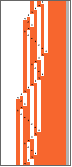
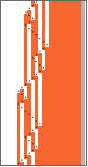
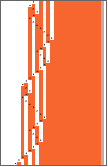
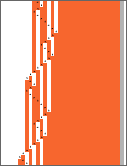
Row[OneSidedTuringMachinePlot[#,"Width"->Length[#[[-1,-1]]]-FirstPosition[#[[-1,-1]],1][[1]]+4,"LabelOutput"->False,ImageSize->40,Mesh->False]&/@Partition[OneSidedTuringMachineEvolution[{1955095,3,2},42,300],50],Spacer[8]]

Out[]=

In[]:=

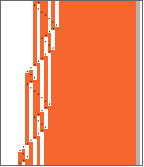
GraphicsRow[OneSidedTuringMachinePlot[#,"Width"->5,"LabelOutput"->False,ImageSize->70,Mesh->False]&/@Partition[OneSidedTuringMachineEvolution[{1955095,3,2},42,300],50]]

Out[]=

In[]:=

#[[1,3]]&/@OneSidedTuringMachineEvolution[{1955095,3,2},42,300]

Out[]=

{0,-1,-2,-3,-4,-5,-6,-7,-6,-5,-6,-7,-6,-5,-4,-3,-2,-1,-2,-3,-4,-5,-4,-3,-2,-3,-4,-5,-6,-7,-8,-9,-8,-7,-8,-9,-8,-7,-6,-5,-4,-3,-4,-5,-6,-7,-6,-5,-4,-5,-6,-7,-8,-9,-10,-11,-10,-9,-10,-11,-10,-9,-8,-7,-6,-5,-6,-7,-8,-9,-8,-7,-6,-7,-8,-9,-10,-11,-12,-13,-12,-11,-12,-13,-12,-11,-10,-9,-8,-7,-8,-9,-10,-11,-10,-9,-8,-9,-10,-11,-12,-13,-14,-15,-14,-13,-14,-15,-14,-13,-12,-11,-10,-9,-10,-11,-12,-13,-12,-11,-10,-11,-12,-13,-14,-15,-16,-17,-16,-15,-16,-17,-16,-15,-14,-13,-12,-11,-12,-13,-14,-15,-14,-13,-12,-13,-14,-15,-16,-17,-18,-19,-18,-17,-18,-19,-18,-17,-16,-15,-14,-13,-14,-15,-16,-17,-16,-15,-14,-15,-16,-17,-18,-19,-20,-21,-20,-19,-20,-21,-20,-19,-18,-17,-16,-15,-16,-17,-18,-19,-18,-17,-16,-17,-18,-19,-20,-21,-22,-23,-22,-21,-22,-23,-22,-21,-20,-19,-18,-17,-18,-19,-20,-21,-20,-19,-18,-19,-20,-21,-22,-23,-24,-25,-24,-23,-24,-25,-24,-23,-22,-21,-20,-19,-20,-21,-22,-23,-22,-21,-20,-21,-22,-23,-24,-25,-26,-27,-26,-25,-26,-27,-26,-25,-24,-23,-22,-21,-22,-23,-24,-25,-24,-23,-22,-23,-24,-25,-26,-27,-28,-29,-28,-27,-28,-29,-28,-27,-26,-25,-24,-23,-24,-25,-26,-27,-26,-25,-24,-25,-26,-27,-28,-29,-30,-31,-30,-29,-30,-31,-30}

In[]:=

Differences[%]

Out[]=

{-1,-1,-1,-1,-1,-1,-1,1,1,-1,-1,1,1,1,1,1,1,-1,-1,-1,-1,1,1,1,-1,-1,-1,-1,-1,-1,-1,1,1,-1,-1,1,1,1,1,1,1,-1,-1,-1,-1,1,1,1,-1,-1,-1,-1,-1,-1,-1,1,1,-1,-1,1,1,1,1,1,1,-1,-1,-1,-1,1,1,1,-1,-1,-1,-1,-1,-1,-1,1,1,-1,-1,1,1,1,1,1,1,-1,-1,-1,-1,1,1,1,-1,-1,-1,-1,-1,-1,-1,1,1,-1,-1,1,1,1,1,1,1,-1,-1,-1,-1,1,1,1,-1,-1,-1,-1,-1,-1,-1,1,1,-1,-1,1,1,1,1,1,1,-1,-1,-1,-1,1,1,1,-1,-1,-1,-1,-1,-1,-1,1,1,-1,-1,1,1,1,1,1,1,-1,-1,-1,-1,1,1,1,-1,-1,-1,-1,-1,-1,-1,1,1,-1,-1,1,1,1,1,1,1,-1,-1,-1,-1,1,1,1,-1,-1,-1,-1,-1,-1,-1,1,1,-1,-1,1,1,1,1,1,1,-1,-1,-1,-1,1,1,1,-1,-1,-1,-1,-1,-1,-1,1,1,-1,-1,1,1,1,1,1,1,-1,-1,-1,-1,1,1,1,-1,-1,-1,-1,-1,-1,-1,1,1,-1,-1,1,1,1,1,1,1,-1,-1,-1,-1,1,1,1,-1,-1,-1,-1,-1,-1,-1,1,1,-1,-1,1,1,1,1,1,1,-1,-1,-1,-1,1,1,1,-1,-1,-1,-1,-1,-1,-1,1,1,-1,-1,1}

In[]:=

FindTransientRepeat[%,3]

Out[]=

{{},{-1,-1,-1,-1,-1,-1,-1,1,1,-1,-1,1,1,1,1,1,1,-1,-1,-1,-1,1,1,1}}

In[]:=

Length/@%

Out[]=

{0,24}

In[]:=

2^20

Out[]=

1048576

In[]:=

f1steps108=With[{s=3,k=2,maxSteps=10^8},ParallelTable[OneSidedTuringMachineFunction[{rule,s,k},1,maxSteps,"Steps"],{rule,0,(2sk)^(sk)-1}]];

Out[]=

$Aborted

In[]:=

f1steps108=With[{s=3,k=2,maxSteps=10^6},ParallelTable[OneSidedTuringMachineFunction[{rule,s,k},1,maxSteps,"Steps"],{rule,0,(2sk)^(sk)-1}]];

In[]:=

f1steps106=

;

In[]:=

CloudExport[f1steps106,"WXF",Permissions->"Public"]

Out[]=

CloudObject[

https://www.wolframcloud.com/obj/6deca4c1-fac1-4fbd-bf79-d89a8c820833

]

In[]:=

Column[Text[Grid[Transpose[Prepend[List@@@Normal[#],{"runtime","machines"}]],Frame->All]]&/@Partition[Normal[KeySort[Counts[f1steps106]]],UpTo[15]]]

Out[]=

runtime	1	3	5	7	9	11	13	15	17	19	21	23	25	27	29
machines	1492992	373248	110592	37008	12432	4516	2278	596	990	314	118	120	30	38	24

runtime	31	33	35	37	41	43	51	53	∞
machines	56	20	4	4	4	4	2	2	950592

In[]:=

f1steps6=f1steps106;

In[]:=

f1steps6=CloudImport[CloudObject[

https://www.wolframcloud.com/obj/6deca4c1-fac1-4fbd-bf79-d89a8c820833

]];

In[]:=

Take[f1steps6,5]

Out[]=

{∞,∞,∞,∞,∞}

In[]:=

allinfs=Flatten[Position[f1steps6,Infinity]-1];

In[]:=

SeedRandom[235234];RandomSample[allinfs,20]

Out[]=

{1142,1610276,561189,234780,1534486,2581180,2642228,1723360,1186347,2159965,2562378,245210,1664396,2713852,2664782,1651506,1221728,1563001,2216422,1182314}

In[]:=

Labeled[OneSidedTuringMachinePlot[{#,3,2},1,{100,10},ImageSize->50,"LabelInput"->True,"LabelOutput"->False],#]&/@{1142,1610276,561189,234780,1534486,2581180,2642228,1723360,1186347,2159965,2562378,245210,1664396,2713852,2664782,1651506,1221728,1563001,2216422,1182314}

Out[]=

