Richard
Richard
In[]:=
PacletInstall["/Users/willemnielsen/Library/CloudStorage/Dropbox-Wolframinstitute/Willem Nielsen/GeneralBox/Blogs/PvsNP/FromRichard/TuringMachinePaclet/TuringMachine-1.0.0.paclet"]
Out[]=
$Failed
ParallelTable[With[{init=IntegerDigits[j,2,10]},TuringMachineRun[{i,3,2},Append[init,0],"FinalFullState","MaxSteps"->10]],{i,2},{j,2}]
Nik
Nik
In[]:=
ParallelMap[Table[TuringMachineFunction[#,i,100],{i,50}]&,EnumerateTuringMachines[1,2]]
Out[]=
{{Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined},{0,Undefined,2,Undefined,4,Undefined,6,Undefined,8,Undefined,10,Undefined,12,Undefined,14,Undefined,16,Undefined,18,Undefined,20,Undefined,22,Undefined,24,Undefined,26,Undefined,28,Undefined,30,Undefined,32,Undefined,34,Undefined,36,Undefined,38,Undefined,40,Undefined,42,Undefined,44,Undefined,46,Undefined,48,Undefined},{Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined},{1,Undefined,3,Undefined,5,Undefined,7,Undefined,9,Undefined,11,Undefined,13,Undefined,15,Undefined,17,Undefined,19,Undefined,21,Undefined,23,Undefined,25,Undefined,27,Undefined,29,Undefined,31,Undefined,33,Undefined,35,Undefined,37,Undefined,39,Undefined,41,Undefined,43,Undefined,45,Undefined,47,Undefined,49,Undefined},{0,2,0,4,4,6,0,8,8,10,8,12,12,14,0,16,16,18,16,20,20,22,16,24,24,26,24,28,28,30,0,32,32,34,32,36,36,38,32,40,40,42,40,44,44,46,32,48,48,50},{0,2,2,4,4,6,6,8,8,10,10,12,12,14,14,16,16,18,18,20,20,22,22,24,24,26,26,28,28,30,30,32,32,34,34,36,36,38,38,40,40,42,42,44,44,46,46,48,48,50},{Undefined,2,Undefined,4,Undefined,6,Undefined,8,Undefined,10,Undefined,12,Undefined,14,Undefined,16,Undefined,18,Undefined,20,Undefined,22,Undefined,24,Undefined,26,Undefined,28,Undefined,30,Undefined,32,Undefined,34,Undefined,36,Undefined,38,Undefined,40,Undefined,42,Undefined,44,Undefined,46,Undefined,48,Undefined,50},{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50},{Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined},{0,0,2,0,4,4,6,0,8,8,10,8,12,12,14,0,16,16,18,16,20,20,22,16,24,24,26,24,28,28,30,0,32,32,34,32,36,36,38,32,40,40,42,40,44,44,46,32,48,48},{Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined,Undefined},{1,3,3,7,5,7,7,15,9,11,11,15,13,15,15,31,17,19,19,23,21,23,23,31,25,27,27,31,29,31,31,63,33,35,35,39,37,39,39,47,41,43,43,47,45,47,47,63,49,51},{3,3,7,5,7,7,15,9,11,11,15,13,15,15,31,17,19,19,23,21,23,23,31,25,27,27,31,29,31,31,63,33,35,35,39,37,39,39,47,41,43,43,47,45,47,47,63,49,51,51},{0,3,2,5,4,7,6,9,8,11,10,13,12,15,14,17,16,19,18,21,20,23,22,25,24,27,26,29,28,31,30,33,32,35,34,37,36,39,38,41,40,43,42,45,44,47,46,49,48,51},{Undefined,3,Undefined,5,Undefined,7,Undefined,9,Undefined,11,Undefined,13,Undefined,15,Undefined,17,Undefined,19,Undefined,21,Undefined,23,Undefined,25,Undefined,27,Undefined,29,Undefined,31,Undefined,33,Undefined,35,Undefined,37,Undefined,39,Undefined,41,Undefined,43,Undefined,45,Undefined,47,Undefined,49,Undefined,51},{1,3,3,5,5,7,7,9,9,11,11,13,13,15,15,17,17,19,19,21,21,23,23,25,25,27,27,29,29,31,31,33,33,35,35,37,37,39,39,41,41,43,43,45,45,47,47,49,49,51}}
In[]:=
ParallelMap[Table[TerminatingTuringMachine[#,i,100,"Steps"],{i,50}]&,EnumerateTuringMachines[1,2]]
Out[]=
{{∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞},{2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞},{∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞},{2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞},{4,2,6,2,4,2,8,2,4,2,6,2,4,2,10,2,4,2,6,2,4,2,8,2,4,2,6,2,4,2,12,2,4,2,6,2,4,2,8,2,4,2,6,2,4,2,10,2,4,2},{2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2},{∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2},{2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2},{∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞},{2,4,2,6,2,4,2,8,2,4,2,6,2,4,2,10,2,4,2,6,2,4,2,8,2,4,2,6,2,4,2,12,2,4,2,6,2,4,2,8,2,4,2,6,2,4,2,10,2,4},{∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞,∞},{2,4,2,6,2,4,2,8,2,4,2,6,2,4,2,10,2,4,2,6,2,4,2,8,2,4,2,6,2,4,2,12,2,4,2,6,2,4,2,8,2,4,2,6,2,4,2,10,2,4},{4,2,6,2,4,2,8,2,4,2,6,2,4,2,10,2,4,2,6,2,4,2,8,2,4,2,6,2,4,2,12,2,4,2,6,2,4,2,8,2,4,2,6,2,4,2,10,2,4,2},{2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2},{∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2,∞,2},{2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2}}
In[]:=
((First/@#)->Last[#[[1]]])&/@GatherBy[ParallelMap[#->Table[TuringMachineFunction[#,i,100],{i,50}]&,EnumerateTuringMachines[1,2]],Last]
Out[]=
In[]:=
res22=((First/@#)->Last[#[[1]]])&/@GatherBy[ParallelMap[#->Table[TuringMachineFunction[#,i,100],{i,50}]&,EnumerateTuringMachines[2,2]],Last];
In[]:=
TakeLargestBy,Total[Last[#]/.Undefined->0]&,5
Out[]=
{{{{1,0}{2,1,-1},{1,1}{2,0,-1},{2,0}{2,1,1},{2,1}{1,0,-1}}}{3,255,31,63,7,31,15,15,11,2047,1023,31,15,1023,127,23,19,511,255,2047,23,255,31,31,27,1023,127,255,31,127,63,39,35,127,63,511,39,63,47,47,43,65535,8191,63,47,8191,4095,55,51,1023},{{{1,0}{2,1,-1},{1,1}{1,1,-1},{2,0}{2,1,1},{2,1}{2,0,-1}}}{31,15,127,15,63,31,511,15,63,31,255,31,127,63,2047,23,63,31,255,31,127,63,1023,31,127,63,511,63,255,127,8191,39,63,47,255,47,127,63,1023,47,127,63,511,63,255,127,4095,55,127,63},{{{1,0}{1,1,-1},{1,1}{2,1,-1},{2,0}{2,1,1},{2,1}{2,0,-1}}}{7,31,15,127,15,63,31,511,15,63,31,255,31,127,63,2047,23,63,31,255,31,127,63,1023,31,127,63,511,63,255,127,8191,39,63,47,255,47,127,63,1023,47,127,63,511,63,255,127,4095,55,127},{{{1,0}{1,1,1},{1,1}{2,0,-1},{2,0}{1,1,-1},{2,1}{1,0,-1}}}{15,3,7,5,511,7,63,9,127,11,15,13,63,15,31,17,31,19,23,21,4095,23,2047,25,63,27,31,29,2047,31,255,33,47,35,39,37,1023,39,511,41,4095,43,47,45,511,47,63,49,63,51},{{{1,0}{2,0,-1},{1,1}{1,1,-1},{2,0}{2,1,1},{2,1}{2,0,-1}}}{15,7,63,7,31,15,255,11,31,15,127,15,63,31,1023,19,31,23,127,23,63,31,511,27,63,31,255,31,127,63,4095,35,47,39,127,39,63,47,511,43,63,47,255,47,127,63,2047,51,63,55}}
In[]:=
Length[res22]
Out[]=
352
In[]:=
TakeLargestBy,Max[Last[#]/.Undefined->0]&,5
Out[]=
{{{{1,0}{2,1,-1},{1,1}{2,0,-1},{2,0}{2,1,1},{2,1}{1,0,-1}}}{3,255,31,63,7,31,15,15,11,2047,1023,31,15,1023,127,23,19,511,255,2047,23,255,31,31,27,1023,127,255,31,127,63,39,35,127,63,511,39,63,47,47,43,65535,8191,63,47,8191,4095,55,51,1023},{{{1,0}{1,1,-1},{1,1}{2,1,-1},{2,0}{2,1,1},{2,1}{2,0,-1}}}{7,31,15,127,15,63,31,511,15,63,31,255,31,127,63,2047,23,63,31,255,31,127,63,1023,31,127,63,511,63,255,127,8191,39,63,47,255,47,127,63,1023,47,127,63,511,63,255,127,4095,55,127},{{{1,0}{2,1,-1},{1,1}{1,1,-1},{2,0}{2,1,1},{2,1}{2,0,-1}}}{31,15,127,15,63,31,511,15,63,31,255,31,127,63,2047,23,63,31,255,31,127,63,1023,31,127,63,511,63,255,127,8191,39,63,47,255,47,127,63,1023,47,127,63,511,63,255,127,4095,55,127,63},{{{1,0}{1,1,-1},{1,1}{2,0,-1},{2,0}{2,1,1},{2,1}{2,0,-1}}}{3,15,7,63,7,31,15,255,11,31,15,127,15,63,31,1023,19,31,23,127,23,63,31,511,27,63,31,255,31,127,63,4095,35,47,39,127,39,63,47,511,43,63,47,255,47,127,63,2047,51,63},{{{1,0}{1,1,1},{1,1}{2,0,-1},{2,0}{1,1,-1},{2,1}{1,0,-1}}}{15,3,7,5,511,7,63,9,127,11,15,13,63,15,31,17,31,19,23,21,4095,23,2047,25,63,27,31,29,2047,31,255,33,47,35,39,37,1023,39,511,41,4095,43,47,45,511,47,63,49,63,51}}
In[]:=
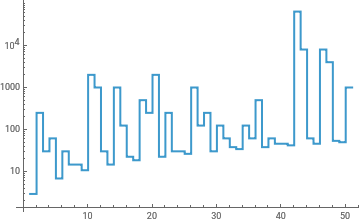
ListStepPlot[{3,255,31,63,7,31,15,15,11,2047,1023,31,15,1023,127,23,19,511,255,2047,23,255,31,31,27,1023,127,255,31,127,63,39,35,127,63,511,39,63,47,47,43,65535,8191,63,47,8191,4095,55,51,1023},ScalingFunctions->"Log"]
Out[]=
Notable cases
Notable cases
Fastest output growth
Fastest output growth
Slowest output growth (constant; then faster; ...)
Slowest output growth (constant; then faster; ...)
Fastest runtime growth
Fastest runtime growth
Fastest space growth
Fastest space growth
Most machines that compute the same function
Most machines that compute the same function
How far does one have to go to disambiguate functions ?
How far does one have to go to disambiguate functions ?
Time Complexity Growth Rates by Input Size
Time Complexity Growth Rates by Input Size
Median Time Complexity Growth Rates by Input Size
Median Time Complexity Growth Rates by Input Size
Means
Means
s=3
s=3
NDTM
NDTM
Given a value of s, k we can form the “everything” machine. In this machine, all we have to do is find how long it takes to make each mapping i -> o
You can set up a write-only machine