In[]:=
ArrayPlot[CellularAutomaton[22,RandomInteger[1,300],200]]
Out[]=
{0,0,0,1,0,0,0}
Particles have a position and a momentum/velocity [ plus perhaps a numerical phase ]
{x,v}|->{x+v,RandomChoice[{p,1-p}->{v,-v}]}
In[]:=
ListLinePlot[First/@With[{p=.9},NestList[({x,v}|->{x+v,RandomChoice[{p,1-p}->{v,-v}]})@@#&,{0,1},50]]]
Out[]=
In[]:=
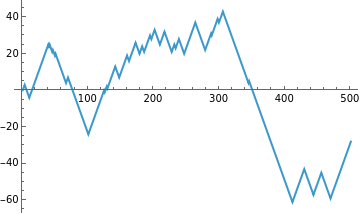
ListLinePlot[First/@With[{p=.9},NestList[({x,v}|->{x+v,RandomChoice[{p,1-p}->{v,-v}]})@@#&,{0,1},500]]]
Out[]=
ListLinePlot[First/@With[{p=.9},NestList[({x,v}|->{x+v,RandomChoice[{p,1-p}->{v,-v}]})@@#&,{0,1},500]]]
In[]:=
Table[With[{p=.9},First@Nest[({x,v}|->{x+v,RandomChoice[{p,1-p}->{v,-v}]})@@#&,{0,1},1000]],1000];
In[]:=
Histogram[%]
Out[]=
Splice
In[]:=
With[{p=.9},NestList[({x,v,ϕ}|->{x+v,Splice[RandomChoice[{p,1-p}->{{v,ϕ},{-v,Iϕ}}]]})@@#&,{0,1,1},20]]
Out[]=
{{0,1,1},{1,1,1},{2,1,1},{3,-1,},{2,-1,},{1,1,-1},{2,1,-1},{3,-1,-},{2,-1,-},{1,-1,-},{0,-1,-},{-1,1,1},{0,1,1},{1,1,1},{2,1,1},{3,1,1},{4,1,1},{5,1,1},{6,1,1},{7,1,1},{8,1,1}}
In[]:=
Lookup[GroupBy[Table[With[{p=.9},Nest[({x,v,ϕ}|->{x+v,Splice[RandomChoice[{p,1-p}->{{v,ϕ},{-v,Iϕ}}]]})@@#&,{0,1,1},20]][[{1,3}]],1000],First->Last,Total],Range[-20,20],0]
Out[]=
{0,0,-2+12,0,-1+10,0,-4+11,0,-7+8,0,-8+4,0,-11,0,-7+9,0,-11+9,0,-17+6,0,-5+7,0,-14,0,-8+3,0,-11+4,0,-15-3,0,-10+8,0,-17+,0,-19+6,0,-23+7,0,-26+5,0,118+19}
In[]:=
Lookup[GroupBy[Table[With[{p=.9},Nest[({x,v,ϕ}|->{x+v,Splice[RandomChoice[{p,1-p}->{{v,ϕ},{-v,Iϕ}}]]})@@#&,{0,1,1},20]][[{1,3}]],10000],First->Last,Total],Range[-20,20,2],0]
Out[]=
{0,-12+108,-26+123,-33+73,-44+47,-43+37,-71+37,-53+22,-60+23,-62+56,-71+38,-64+29,-78-4,-113+3,-122+38,-132+6,-182+47,-181+62,-230+90,-313+104,1187+118}
In[]:=
ListLinePlot[Abs[%]]
Out[]=
In[]:=
ListLinePlot[Arg[%32]]
Out[]=
Make a multiway system for the random walk
In[]:=
(Graph[#1,VertexCoordinates->(#1->#1&)/@VertexList[#1],VertexSize->0.15]&)[NestGraph[Function[p,{p+{1,0},p+{-1,0},p+{0,1},p+{0,-1}}],{{0,0}},4,EdgeStyle->Gray,VertexStyle->Directive[EdgeForm[GrayLevel[0.4]],GrayLevel[0.7]]]]
Out[]=
Massive propagator
Massive propagator
Momentum space:
1/p^2
In[]:=
Table[PathGraph[Range[i]],{i,2,5}]
Out[]=
{
,
,
,
}
In[]:=
Sum[m^(2k)1/(p^2)^(k+1),{k,0,Infinity}]
Out[]=
1
-+
2
m
2
p
In position space, a zig-zag is the analog of a mass insertion
In the universal causal graph, any causal edge that doesn’t interact is going at the speed of light [definition of speed of light]
String version of Feynman checkerboard
String version of Feynman checkerboard
Might want to have more Turing machine like system...