In[]:=
$MachineName
Out[]=
threadripper2
In[]:=
rhmr=Module[{ru={299459058088077823758143088095350287424,4,1},init={{1},0},txspec={200,{-110,110}},aps,pca,ca},SeedRandom[444666];ParallelMap[#->HealCA[ru,init,txspec,#,1,#==101&,"Order"->"Random"]&,allperts[CellularAutomaton[ru,init,txspec]]]];
In[]:=
alltrainr=With[{ru={299459058088077823758143088095350287424,4,1},init={{1},0},txspec={200,{-110,110}}},(If[#=={},0,#[[2]]-#[[1]]+1]&[nonzeroRange[#]]&/@First[PerturbedCellularAutomaton[ru,init,{Keys[First[#]][[1,1]],{-110,110}}]])->If[Last[#]==={},{},Keys[Last[#][[1]]][[1]]]]&/@rhmr
Out[]=
In[]:=
alltrain2r=Discard[alltrainr,Last[#]==={}&];
In[]:=
alltrain2=;
In[]:=
alltrain2=;
In[]:=
alltrain2[[;;3]]
Out[]=
{{1}{52,122}0,{1,0}{92,115}0,{1,3,2}{3,112}1}
In[]:=
goals=#[[1]]->First[KeyValueMap[Append,#[[2]]]]&/@alltrain2;
In[]:=
Take[goals,5]
Out[]=
{{1}{52,122,0},{1,0}{92,115,0},{1,3,2}{3,112,1},{1,1,0}{3,110,2},{1,1,3}{3,112,0}}
In[]:=
SeedRandom[24234];data=RandomSample[goals,2000]
Out[]=
In[]:=
SeedRandom[224];tdgoals=goals[[#]]&/@TakeDrop[RandomSample[Range[Length[goals]]],2000];
In[]:=
Iconize[SeedRandom[224];TakeDrop[RandomSample[Range[Length[goals]]],2000]]
Out[]=
[[ moved to 24a as casemap ]]
In[]:=
Length[tdgoals]
Out[]=
2
In[]:=
traingoals=tdgoals[[1]];
In[]:=
testgoals=tdgoals[[2]];
In[]:=
length=Max[Length@*First/@goals]
Out[]=
101
In[]:=
padtrain=MapAt[PadRight[#,length,-1]&,traingoals,{All,1}]
Out[]=
In[]:=
padtest=MapAt[PadRight[#,length,-1]&,testgoals,{All,1}]
Out[]=
In[]:=
net=NetInitialize@NetChain[{32,Tanh,16,Tanh,3},"Input"->length]
Out[]=
NetChain
In[]:=
netTrained=NetTrain[net,padtrain,TargetDevice->"GPU"];
In[]:=
netTrained=NetTrain[netTrained,padtrain,TargetDevice->"GPU"];
In[]:=
ListPointPlot3D[{netTrained[padtest[[All,1]]],padtest[[All,2]]}]
Out[]=
In[]:=
predictions=Thread[{netTrained[padtest[[All,1]]][[All,#]],padtest[[All,2,#]]}]&/@{1,2,3}
Out[]=
In[]:=
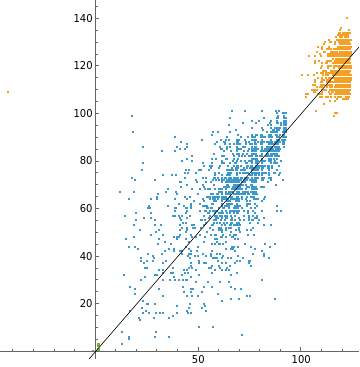
ListPlot[predictions,AspectRatio->1,PlotRange->Full,Epilog->InfiniteLine[{{0,0},{1,1}}]]
Out[]=