In[]:=
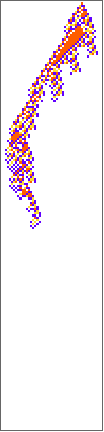
bigyellow={297413941736400589979939780692294751544,4,1};
In[]:=
PlotCA[bigyellow]
Out[]=
In[]:=
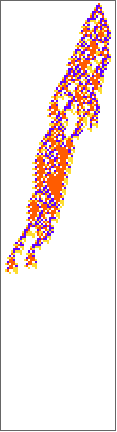
bigred={201412842028162214137229450141139961424,4,1};
In[]:=
PlotCA[bigred]
Out[]=
In[]:=
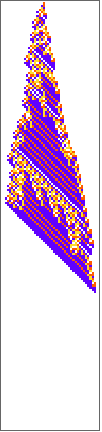
cands=DeleteDuplicates@
;ru=cands[[13]];ca=getca[cands[[13]],200];
In[]:=
PlotCA/@cands
Out[]=

,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,

In[]:=
SetOptions[ListPlot,PlotHighlighting->None];

New Silhouette Functions

Cleaner and Faster CAMask

Single ca

In[]:=
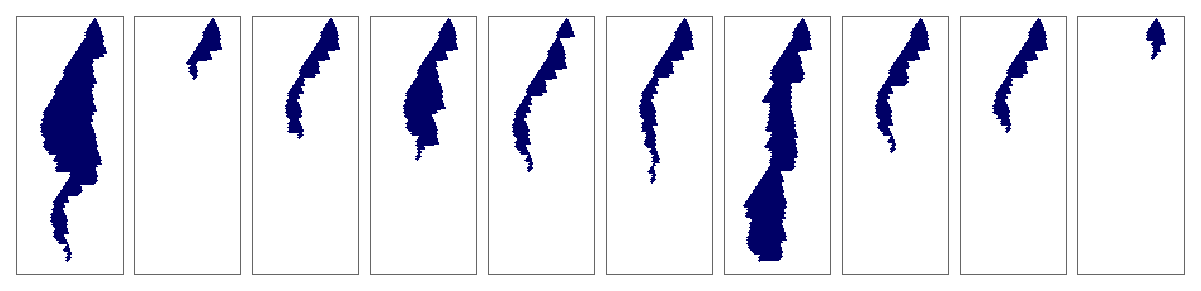
GraphicsRow[With[{ca=getca[ru,{200,{-50,60}}]},CAMask[#,"Color"->Darker[Blue,0.6],"Trim"->{None,None}]&/@(PerturbCA[{ca,ru},#,"ReturnPerturbations"->False]&/@RandomSample[allperts[ca],10])]]

All perturbations merged

With[{ca=getca[cands[[13]],{200,{-30,45}}]},CAMask[PerturbCA[{ca,cands[[13]]},#,"ReturnPerturbations"->False]&/@allperts[ca][[All]],"Color"->Darker[Blue,0.6],"Trim"->{None,None}]]
Out[]=

Other interesting rule

With[{ca=getca[ru,{200,{-50,20}}]},CAMask[PerturbCA[{ca,ru},#,"ReturnPerturbations"->False]&/@allperts[ca],"Color"->Darker[Blue,0.6]]]
Out[]=
In[]:=
GraphicsRow[With[{ca=getca[cands[[9]],{200,{-60,20}}]},CAMask[#,"Color"->Darker[Blue,0.6],"Trim"->{None,None}]&/@(PerturbCA[{ca,cands[[9]]},#,"ReturnPerturbations"->False]&/@RandomSample[allperts[ca],10])]]
Out[]=
TODO: Make mean plot more sensitive so you can see the perturbations more (Try Log?)

Polygon version

Multi-color

3D Stack (Fossil drawer)

Overlayed Polygon on all candidates

Overlayed outline

Single

Comparing Widths With Lifetimes at all steps

Predicting Lifetime Based on Width

Step 70

Loss

Step 100

Loss

Step 30

Loss

Predicting based on row sequence

Loss

Step 30

Loss

Predicting Lifetime Based on Non-Zero Range sequence

Predicting Widths based on previous widths

Click to copy ideas