In[]:=
∂
t,t
3/2
(+)
2
z[t]
2
(1/2(1+eSin[2πt]))
Out[]=
′′
z
z[t]
3/2
+
1
4
2
(1+eSin[2πt])
2
z[t]
In[]:=
Clear[z]
In[]:=
NDSolveValuez[t]==-z[t],z'[0]==0,z[0]==.1,z,{t,0,50}
∂
t,t
3/2
(+)
2
z[t]
2
(1/2(1+1/2Sin[2πt]))
Out[]=
InterpolatingFunction
In[]:=
Plot[%[t],{t,0,50}]
Out[]=
In[]:=
NDSolveValuez[t]==-z[t],z'[0]==0,z[0]==110,z,{t,0,50},WorkingPrecision->50,MaxSteps->10^6
∂
t,t
3/2
(+)
2
z[t]
2
(1/2(1+1/2Sin[2πt]))
Out[]=
InterpolatingFunction
In[]:=
Plot[%271[t],{t,0,14}]
Out[]=
In[]:=
Plot[%268[t]-%271[t],{t,0,14}]
Out[]=
In[]:=
NDSolveValuez[t]==-z[t],z'[0]==0,z[0]==110,z,{t,0,50},WorkingPrecision->50,MaxSteps->10^7
∂
t,t
3/2
(+)
2
z[t]
2
(1/2(1+1/2Sin[2πt]))
Out[]=
InterpolatingFunction
In[]:=
NDSolveValuez[t]==-z[t],z'[0]==0,z[0]==110,z,{t,0,50},WorkingPrecision->100,MaxSteps->10^7
∂
t,t
3/2
(+)
2
z[t]
2
(1/2(1+1/2Sin[2πt]))
Out[]=
InterpolatingFunction
In[]:=
Plot[%268[t]-%276[t],{t,0,33}]
Eccentricity 1
Eccentricity 1
NDSolveValuez[t]==-z[t],z'[0]==0,z[0]==.1,z,{t,0,50}
∂
t,t
3/2
(+)
2
z[t]
2
(1/2(1+Sin[2πt]))
Out[]=
InterpolatingFunction
In[]:=
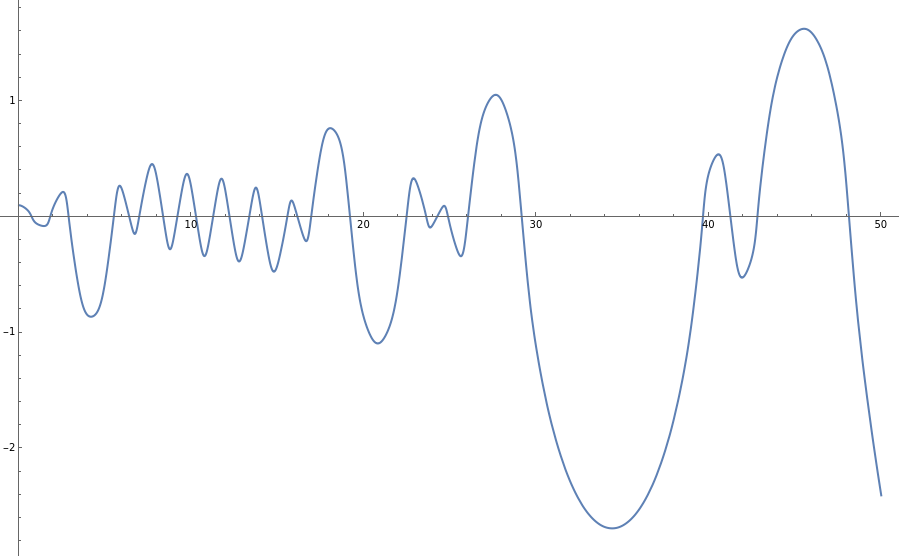
Plot[%[t],{t,0,50}]
Out[]=
Programmability
Programmability
For what value of z[0] is the trajectory easy to predict?
In[]:=
NestList[x|->FractionalPart[2x],FromDigits[{{1,0,1,1,0,1,1,1,0},-1},2],20]
Out[]=
,,,,,,,,,0,0,0,0,0,0,0,0,0,0,0,0
183
512
183
256
55
128
55
64
23
32
7
16
7
8
3
4
1
2
In[]:=
IntegerPart[2%]
Out[]=
{0,1,0,1,1,0,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0}