You are using a browser not supported by the Wolfram Cloud
Supported browsers include recent versions of Chrome, Edge, Firefox and Safari.
I understand and wish to continue anyway »
WOLFRAM NOTEBOOK
In[]:=
First/@SplitByModule{goal=40,deep=5000,cut=100,ru,life,evo},SeedRandom[422772];evo=NestListCompoundExpressionru=[First[#]],life=[ru,cut],If[life!=-Infinity&&Abs[life-goal]<=Abs[Last[#]-goal],{ru,life},#]&,{{0,3,1},1},deep,Last
Out[]=
{{{0,3,1},1},{{249,3,1},2},{{5277861284793,3,1},3},{{5557966652634,3,1},4},{{6433305833670,3,1},5},{{5781409302345,3,1},6},{{6543746120886,3,1},12},{{6564665232969,3,1},20}}
In[]:=
ParallelTableFirst/@SplitByModule{goal=40,deep=5000,cut=100,ru,life,evo},SeedRandom[422772+i];evo=NestListCompoundExpressionru=[First[#]],life=[ru,cut],If[life!=-Infinity&&Abs[life-goal]<=Abs[Last[#]-goal],{ru,life},#]&,{{0,3,1},1},deep,Last,{i,32}
Out[]=
In[]:=
Last/@%
Out[]=
{{{7194677830917,3,1},30},{{4393704222792,3,1},42},{{7158935779179,3,1},16},{{3256973177433,3,1},45},{{7258376880861,3,1},42},{{7256308571133,3,1},18},{{4192469773107,3,1},32},{{7308383527914,3,1},46},{{1595969514468,3,1},42},{{4370736492810,3,1},43},{{2630310597735,3,1},37},{{3019875037449,3,1},45},{{4466629270257,3,1},35},{{4297080343281,3,1},45},{{5551323019026,3,1},19},{{2058655981686,3,1},39},{{6577450091691,3,1},20},{{4644587426424,3,1},30},{{4294696417242,3,1},29},{{3224218902012,3,1},28},{{3575342072094,3,1},33},{{1623743329281,3,1},48},{{4675829605083,3,1},38},{{2530436489604,3,1},25},{{1384515631068,3,1},47},{{5402257963188,3,1},34},{{3608966757534,3,1},37},{{4465620415473,3,1},22},{{4134447104316,3,1},37},{{7507576087803,3,1},19},{{4361391916389,3,1},35},{{2831595466461,3,1},37}}
ParallelTable
In[]:=
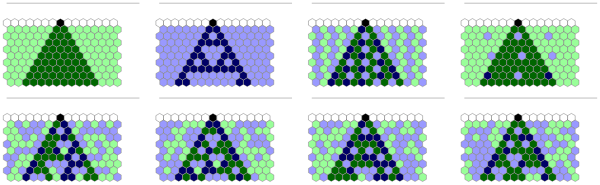
With[{raHeight=9,raWidth=15},GraphicsGrid[Partition[With[{rules={14,6},opts=Sequence["Radius"->1/2,"Orientation"->"Both","Mesh"->True,Appearance->"Hexagonal"],ruleArray=#},ICAEvolutionPlot[raHeight,raWidth,ruleArray,rules,CenterArray[1,{raWidth}],opts,Epilog->{Opacity[0.25],Line[{{0,raHeight},{raWidth,raHeight}}]}]]&/@Join[{Table[1,raHeight,raWidth],Table[2,raHeight,raWidth],Table[Mod[x+y,2,1],{x,raHeight},{y,raWidth}],Table[If[Divisible[x+1,3]&&Divisible[y,4],2,1],{x,raHeight},{y,raWidth}]},Table[SeedRandom[i];Table[RandomChoice[{1,2}],raHeight,raWidth],{i,{101,102,103,105}}]],4]]]
Out[]=
Function Evaluation
Function Evaluation
In[]:=
With[{raHeight=30,raWidth=20,rules={6,8},opts=Sequence["Radius"->1/2,"Orientation"->"Both","Neighborhood"->"Alternating","Appearance"->"Hexagonal"]},With[{raOpts=Sequence@@FilterRules[{opts},Options[RuleArray]]},With[{fn=(x|->Rescale[oneZeroOneOneFunction[Rescale[x,{1,raWidth},{-3,3}]],{0,1},{Floor[raWidth*1/4],Floor[raWidth*3/4]}]),finalStateFn=RuleArrayFinalState[raOpts]},With[{seed=30498503+1},Block[{},SeedRandom[seed];With[{loss=FunctionWithZerosLoss[fn]},With[{lossFn=loss[raHeight,raWidth,raOpts]},res=AdaptRuleArray[ConstantArray[2,{raHeight,raWidth}],rules,40000,lossFn,raOpts];];]]]]]];
In[]:=
CloudExport[res,"WXF"]
Out[]=
In[]:=
AbsoluteTiming[fstates=Table[RuleArrayStates["Radius"->1/2,"Orientation"->"Both","Neighborhood"->"Alternating"][UnitVector[20,n],IndicesToRules[First[Last[res]],{6,8}],30],{n,20}];]
Out[]=
{0.001618,Null}
In[]:=
Dimensions[fstates]
Out[]=
{20,31,20}
In[]:=
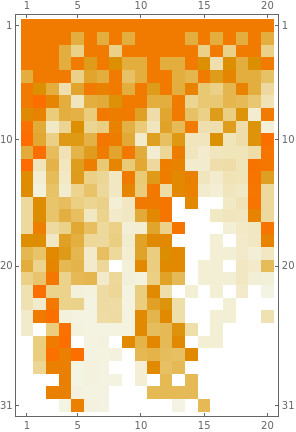
MatrixPlot[ArrayReduce[Mean,fstates,1]]
Out[]=
In[]:=
SeedRandom[2424];MatrixPlot[ArrayReduce[Mean,RuleArrayStates["Radius"->1/2,"Orientation"->"Both","Neighborhood"->"Alternating"][#,IndicesToRules[First[Last[res]],{6,8}],30]&/@Tuples[{1,0},20],1]]
Out[]=
In[]:=
Mean[With[{ra=IndicesToRules[First[Last[res]],{6,8}]},RuleArrayFinalState["Radius"->1/2,"Orientation"->"Both","Neighborhood"->"Alternating"][#,ra,30]&/@Tuples[{1,0},20]]]
Out[]=
0,0,0,,,,,0,0,0,0,0,,0,,0,0,0,0,0
75
1048576
247059
524288
779
524288
125
1048576
33
1048576
14093
65536
Consensus
Consensus
Nand, Nor
Nand, Nor
x axis : input density ; y axis : output density
As a function of time, the gaggle of IntegerDigits corresponding to output states at that time....
Net Testing
Net Testing