In[]:=
Module[{deep=5000,cut=200,ru,life,evo,data},SeedRandom[426778];evo=NestList[CompoundExpression[ru=RandomRuleMutation[First[#]],life=TestLifetime[ru,cut],If[life>=Last[#],{ru,life},#]]&,{{0,3,1},0},deep];evo=Rest[First/@SplitBy[evo,Last]];Map[CompoundExpression[data=CellularAutomaton[First[#],{{1},0},Last[#]+2],data=ArrayPad[#,2]&/@data,ArrayPlot[data,ColorRules->colors,ImageSize->{Automatic,26Sqrt[Length[data]+1]},Mesh->True,MeshStyle->Opacity[.1]]]&,evo]]
In[]:=
MaximalBy[IterateMutations[1,GreaterEqual][{{0,3,1},1}],Last]
Out[]=
{{{39366,3,1},2},{{54,3,1},2},{{6,3,1},2}}
In[]:=
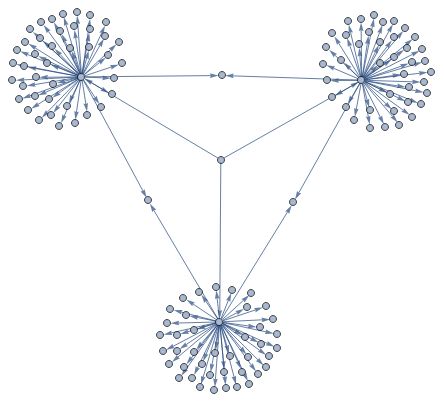
NestGraph[MaximalBy[IterateMutations[1,GreaterEqual][#],Last]&,{{{0,3,1},1}},2]
Out[]=
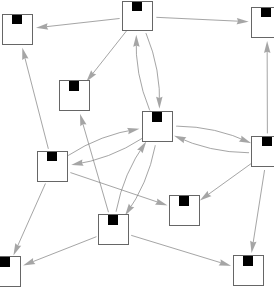
In[]:=
NestGraph[MaximalBy[IterateMutations[1,GreaterEqual][#],Last]&,{{{0,2,1},1}},2,VertexSize->2/4,EdgeStyle->Gray,VertexShapeFunction->Function[Inset[ArrayPlot[ArrayPad[#,1]&/@CellularAutomaton[#2[[1]],{{1},0},#2[[2]]+1],ColorRules->{0->White,1->Black}],#1,Automatic,{Automatic,Last[#3]Sqrt[(#2[[2]]+2)]}]]]
Out[]=
In[]:=
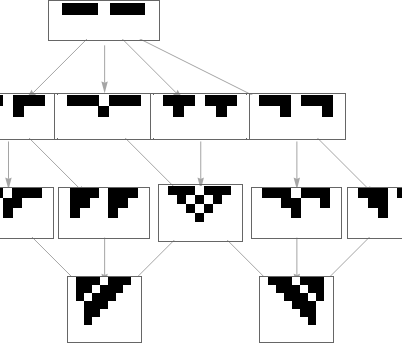
With[{init={1,1,1,0,1,1,1}},NestGraph[MaximalBy[IterateMutations[1,GreaterEqual][#,init],Last]&,{{{0,2,1},1}},4,VertexSize->2/4,EdgeStyle->Gray,VertexShapeFunction->Function[Inset[ArrayPlot[ArrayPad[#,1]&/@CellularAutomaton[#2[[1]],{init,0},#2[[2]]+1],ColorRules->{0->White,1->Black}],#1,Automatic,{Automatic,Last[#3]Sqrt[(#2[[2]]+2)]}]]]]
Out[]=
In[]:=
With[{init={1,1,1,0,1,1,1}},NestGraph[MaximalBy[IterateMutations[1,GreaterEqual][#,init],Last]&,{{{0,2,3/2},1}},2,VertexSize->2/4,EdgeStyle->Gray,VertexShapeFunction->Function[Inset[ArrayPlot[ArrayPad[#,1]&/@CellularAutomaton[#2[[1]],{init,0},#2[[2]]+1],ColorRules->{0->White,1->Black}],#1,Automatic,{Automatic,Last[#3]Sqrt[(#2[[2]]+2)]}]]]]
Out[]=
In[]:=
With[{init={1,1}},NestGraph[MaximalBy[IterateMutations[1,GreaterEqual][#,init],Last]&,{{{0,2,3/2},1}},2,VertexSize->2/4,EdgeStyle->Gray,VertexShapeFunction->Function[Inset[ArrayPlot[ArrayPad[#,1]&/@CellularAutomaton[#2[[1]],{init,0},#2[[2]]+1],ColorRules->{0->White,1->Black}],#1,Automatic,{Automatic,Last[#3]Sqrt[(#2[[2]]+2)]}]]]]
Out[]=
RandomChoice[MaximalBy[IterateMutations[1,GreaterEqual][{{0,3,1},1}],Last]]
Module[{deep=5000,cut=200,ru,life,evo,data},SeedRandom[426778];evo=NestList[CompoundExpression[ru=RandomRuleMutation[First[#]],life=TestLifetime[ru,cut],If[life>=Last[#],{ru,life},#]]&,{{0,3,1},0},deep];evo=Rest[First/@SplitBy[evo,Last]];Map[CompoundExpression[data=CellularAutomaton[First[#],{{1},0},Last[#]+2],data=ArrayPad[#,2]&/@data,ArrayPlot[data,ColorRules->colors,ImageSize->{Automatic,26Sqrt[Length[data]+1]},Mesh->True,MeshStyle->Opacity[.1]]]&,evo]]
Greater Fitness
Greater Fitness
Single always-great mutation can’t get anywhere....
If allow two mutations at a time, can get somewhere
At every step, we pick at random a mutation that strictly increases fitness; if none exists, we stop...
Peel Off Maximum
Peel Off Maximum
Include Lower Fitness
Include Lower Fitness