Adaptation with Perturbation-Based Fitness
Adaptation with Perturbation-Based Fitness
In[]:=
randomrulemutation=;
Doing Ceiling[lifetime/20] permutations and taking the fitness to be their min....
In[]:=
evo42=Module[{ru,ca,lt,pcas,fitness},SeedRandom[426778];NestList[CompoundExpression[ru=randomrulemutation[First[#]],ca=CellularAutomaton[ru,{{1},0},{200,All}];lt=TestCALifeTime[ca];If[lt==-Infinity,#,(*pcas=Table[PerturbCA[{ca,ru}],Ceiling[lt/20]];*)pcas=Table[PerturbCAFast[{ca,ru},"Random"->1,lt],Ceiling[lt/20]];fitness=Min[Join[{lt},TestCALifeTime/@pcas]];If[fitness>=Last[#],{ru,fitness},#]]]&,{{0,4,1},0},2000]];
In[]:=
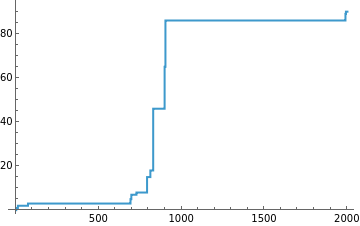
ListStepPlot[Last/@evo42]
Out[]=
In[]:=
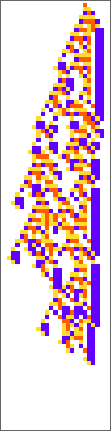
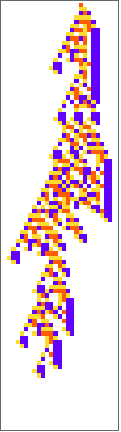
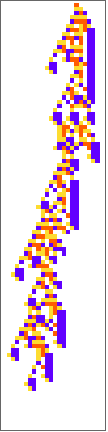
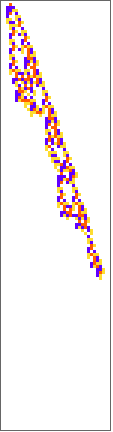
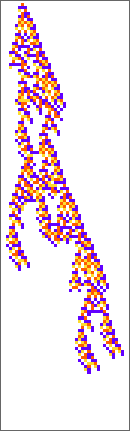
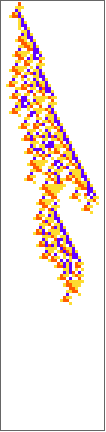
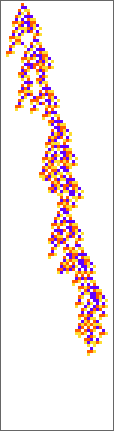
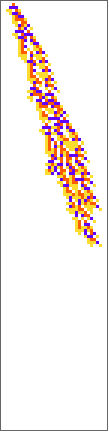
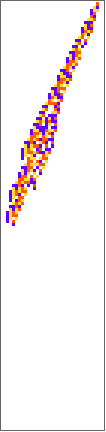
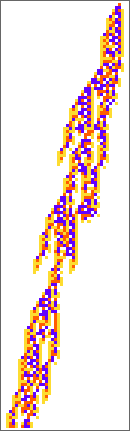
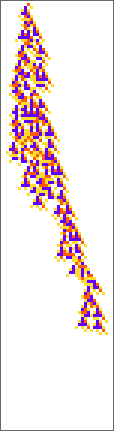
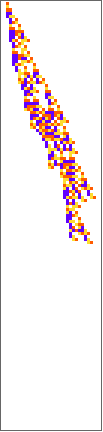
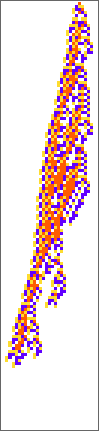
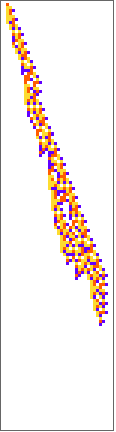
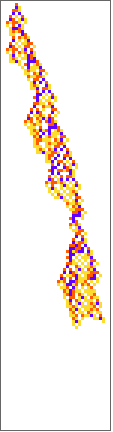
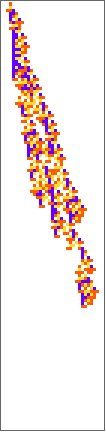
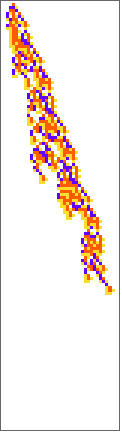
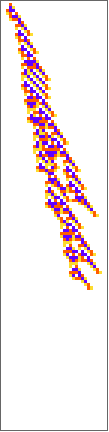
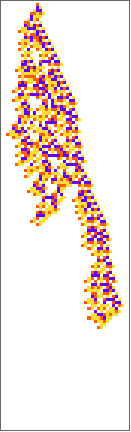
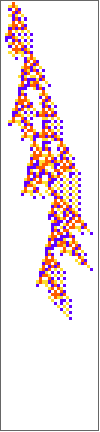
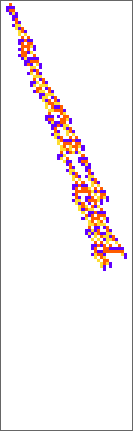
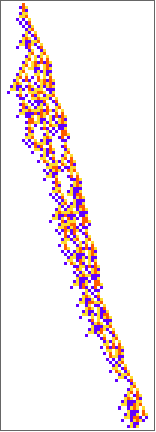
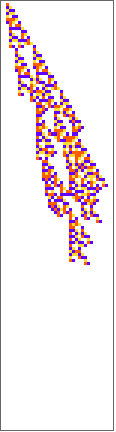
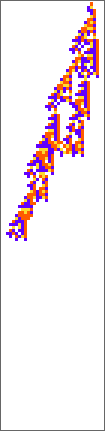
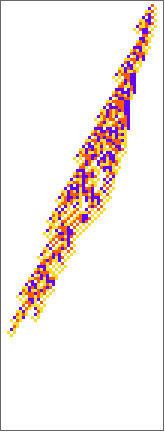
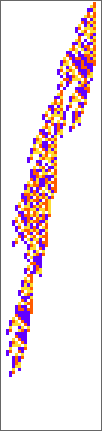
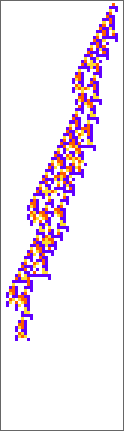
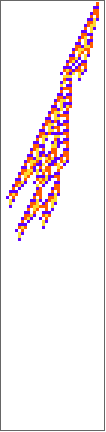
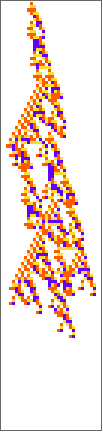
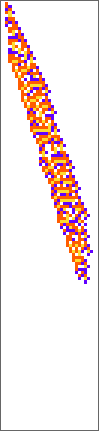
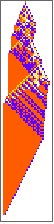
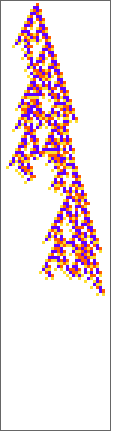
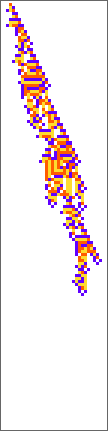
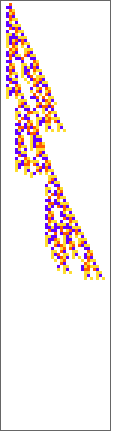
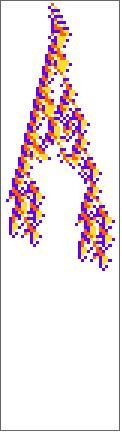
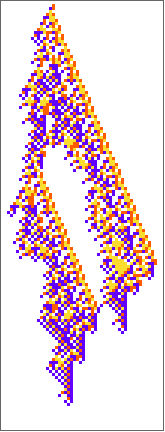
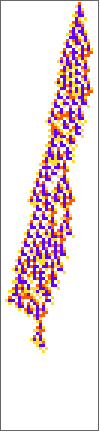
PlotCA[#[[1,1]],"steps"->100,"init"->{{1},0}]&/@SplitBy[evo42,Last]
Out[]=
,
,
,
,
,
,
,
,
,
,
,
,
,
In[]:=
ParallelTable[Module[{ru,ca,lt,pcas,fitness},SeedRandom[426778+i];NestList[CompoundExpression[ru=randomrulemutation[First[#]],ca=CellularAutomaton[ru,{{1},0},{200,All}];lt=TestCALifeTime[ca];If[lt==-Infinity,#,(*pcas=Table[PerturbCA[{ca,ru}],Ceiling[lt/20]];*)pcas=Table[PerturbCAFast[{ca,ru},"Random"->1,lt],Ceiling[lt/20]];fitness=Min[Join[{lt},TestCALifeTime/@pcas]];If[fitness>=Last[#],{ru,fitness},#]]]&,{{0,4,1},0},2000]]//Last,{i,200}]
Out[]=
In[]:=
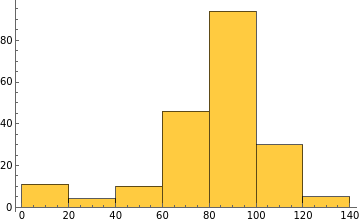
Histogram[Last/@%]
Out[]=
In[]:=
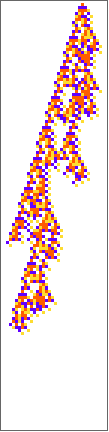
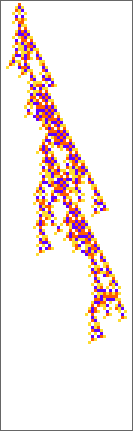
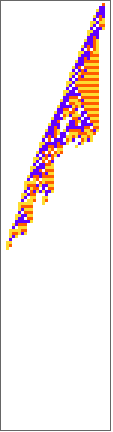
PlotCA[First[#],"steps"->140,"init"->{{1},0}]&/@
Out[]=
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
Compare with no perturbations
Non-Robust Adaptation
Non-Robust Adaptation
Evolving with Fitness Function of Perturbation-Robust Lifetime
Evolving with Fitness Function of Perturbation-Robust Lifetime
Ordinary case:
Ordinary case: