In[]:=
CloudGet["https://www.wolframcloud.com/obj/sw-blog/MultiwayTuringMachines/Programs-01.wl"];
In[]:=
MWTMBushiness[rule_,tmax_]:=If[SameQ@@#,First[#],Infinity]&[Table[VertexCount[MultiwayTuringMachine[List/@rule,{{1,t+1,0},Table[0,2t+1]},t,"StatesGraphStructure"]],{t,tmax,tmax+1}]]
In[]:=
MWTMAdaptiveList[initrule_,{s_,k_},init_,tmax_,smax_]:=NestList[With[{u=TMMutation[First[#],{s,k}]},With[{b=MWTMBushiness[u,tmax]},If[b!=Infinity&&b>=Last[#],{u,b},#]]]&,{initrule,MWTMBushiness[initrule,tmax]},smax]
In[]:=
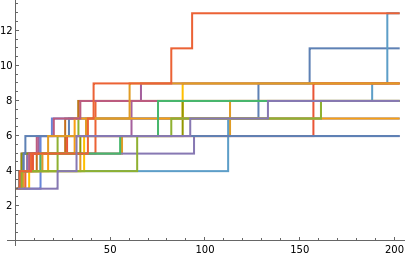
ParallelTable[SeedRandom[9238742089734+i];MWTMAdaptiveList[Join[#,{#[[1]]}]&[InitTM[{2,2}]],{2,2},Null,10,200],{i,20}]
Out[]=
{{{{{1,0}{0,0,0},{1,1}{0,1,0},{2,0}{0,0,0},{2,1}{0,1,0},{1,0}{0,0,0}},3},{{{1,0}{0,0,0},{1,1}{0,1,0},{2,0}{0,0,0},{2,1}{0,1,0},{1,0}{0,0,-1}},4},{{{1,0}{0,0,0},{1,1}{0,1,0},{2,0}{0,0,0},{2,1}{2,1,0},{1,0}{0,0,-1}},4},{{{1,0}{0,0,0},{1,1}{0,1,0},{2,0}{0,0,0},{2,1}{2,1,0},{1,0}{2,0,-1}},5},{{{1,0}{0,0,0},{1,1}{0,1,0},{2,0}{0,0,0},{2,1}{2,1,0},{1,0}{2,1,-1}},5},
⋯192⋯
,{{{1,0}{1,1,0},{1,1}{0,0,1},{2,0}{1,1,-1},{2,1}{1,1,0},{1,0}{2,0,1}},11},{{{1,0}{1,1,0},{1,1}{0,0,1},{2,0}{1,1,-1},{2,1}{1,1,0},{1,0}{2,0,1}},11},{{{1,0}{1,1,0},{1,1}{0,0,1},{2,0}{1,1,-1},{2,1}{1,1,0},{1,0}{2,0,1}},11},{{{1,0}{1,1,0},{1,1}{0,0,1},{2,0}{1,1,-1},{2,1}{1,1,0},{1,0}{2,0,1}},11}},{
⋯1⋯
},
⋯16⋯
,{
⋯1⋯
},{
⋯1⋯
}}
Full expression not available
(
original memory size:
5.8 MB)
In[]:=
ListStepPlotLast/@#&/@
,PlotRange->All
Out[]=
In[]:=
InitTM[{2,2}]
Out[]=
{{1,0}{0,0,0},{1,1}{0,1,0},{2,0}{0,0,0},{2,1}{0,1,0}}
In[]:=
Union[First/@AllTM[2,2]]
Out[]=
{{1,0}{0,0,-1},{1,0}{0,0,1},{1,0}{0,1,-1},{1,0}{0,1,1},{1,0}{1,0,-1},{1,0}{1,0,1},{1,0}{1,1,-1},{1,0}{1,1,1},{1,0}{2,0,-1},{1,0}{2,0,1},{1,0}{2,1,-1},{1,0}{2,1,1}}
In[]:=
Catenate[Table[Union[#[[i]]&/@AllTM[2,2]],{i,4}]]
Out[]=
{{1,0}{0,0,-1},{1,0}{0,0,1},{1,0}{0,1,-1},{1,0}{0,1,1},{1,0}{1,0,-1},{1,0}{1,0,1},{1,0}{1,1,-1},{1,0}{1,1,1},{1,0}{2,0,-1},{1,0}{2,0,1},{1,0}{2,1,-1},{1,0}{2,1,1},{1,1}{0,0,-1},{1,1}{0,0,1},{1,1}{0,1,-1},{1,1}{0,1,1},{1,1}{1,0,-1},{1,1}{1,0,1},{1,1}{1,1,-1},{1,1}{1,1,1},{1,1}{2,0,-1},{1,1}{2,0,1},{1,1}{2,1,-1},{1,1}{2,1,1},{2,0}{0,0,-1},{2,0}{0,0,1},{2,0}{0,1,-1},{2,0}{0,1,1},{2,0}{1,0,-1},{2,0}{1,0,1},{2,0}{1,1,-1},{2,0}{1,1,1},{2,0}{2,0,-1},{2,0}{2,0,1},{2,0}{2,1,-1},{2,0}{2,1,1},{2,1}{0,0,-1},{2,1}{0,0,1},{2,1}{0,1,-1},{2,1}{0,1,1},{2,1}{1,0,-1},{2,1}{1,0,1},{2,1}{1,1,-1},{2,1}{1,1,1},{2,1}{2,0,-1},{2,1}{2,0,1},{2,1}{2,1,-1},{2,1}{2,1,1}}
In[]:=
Length[AllTM[2,2]]
Out[]=
20736
In[]:=
Length[%88]
Out[]=
48
In[]:=
Length[%85]
Out[]=
12
In[]:=
allmwtm=Catenate[Outer[Append,AllTM[2,2],Union[First/@AllTM[2,2]],1]];
In[]:=
First[%]
Out[]=
{{1,0}{0,0,-1},{1,1}{0,0,-1},{2,0}{0,0,-1},{2,1}{0,0,-1},{1,0}{0,0,-1}}
In[]:=
uallmwtm=Union[Sort/@allmwtm];
In[]:=
Length[%]
Out[]=
134784
In[]:=
ParallelMap[#->MWTMBushiness[#,10]&,uallmwtm];
In[]:=
KeySort[Counts[Last/@%]]
Out[]=
37200,413872,510112,65154,7354,8430,9132,10176,1140,1516,1616,∞97282
In[]:=
First/@Select
76
,Last[#]==16&
Out[]=
{{{1,0}{2,0,-1},{1,0}{2,1,-1},{1,1}{2,0,1},{2,0}{1,1,1},{2,1}{0,0,-1}},{{1,0}{2,0,-1},{1,0}{2,1,-1},{1,1}{2,0,1},{2,0}{1,1,1},{2,1}{0,0,1}},{{1,0}{2,0,-1},{1,0}{2,1,-1},{1,1}{2,0,1},{2,0}{1,1,1},{2,1}{0,1,-1}},{{1,0}{2,0,-1},{1,0}{2,1,-1},{1,1}{2,0,1},{2,0}{1,1,1},{2,1}{0,1,1}},{{1,0}{2,0,-1},{1,0}{2,1,-1},{1,1}{2,1,1},{2,0}{1,1,1},{2,1}{0,0,-1}},{{1,0}{2,0,-1},{1,0}{2,1,-1},{1,1}{2,1,1},{2,0}{1,1,1},{2,1}{0,0,1}},{{1,0}{2,0,-1},{1,0}{2,1,-1},{1,1}{2,1,1},{2,0}{1,1,1},{2,1}{0,1,-1}},{{1,0}{2,0,-1},{1,0}{2,1,-1},{1,1}{2,1,1},{2,0}{1,1,1},{2,1}{0,1,1}},{{1,0}{2,0,1},{1,0}{2,1,1},{1,1}{2,0,-1},{2,0}{1,1,-1},{2,1}{0,0,-1}},{{1,0}{2,0,1},{1,0}{2,1,1},{1,1}{2,0,-1},{2,0}{1,1,-1},{2,1}{0,0,1}},{{1,0}{2,0,1},{1,0}{2,1,1},{1,1}{2,0,-1},{2,0}{1,1,-1},{2,1}{0,1,-1}},{{1,0}{2,0,1},{1,0}{2,1,1},{1,1}{2,0,-1},{2,0}{1,1,-1},{2,1}{0,1,1}},{{1,0}{2,0,1},{1,0}{2,1,1},{1,1}{2,1,-1},{2,0}{1,1,-1},{2,1}{0,0,-1}},{{1,0}{2,0,1},{1,0}{2,1,1},{1,1}{2,1,-1},{2,0}{1,1,-1},{2,1}{0,0,1}},{{1,0}{2,0,1},{1,0}{2,1,1},{1,1}{2,1,-1},{2,0}{1,1,-1},{2,1}{0,1,-1}},{{1,0}{2,0,1},{1,0}{2,1,1},{1,1}{2,1,-1},{2,0}{1,1,-1},{2,1}{0,1,1}}}
In[]:=
With[{t=10},MultiwayTuringMachine[List/@#,{{1,t+1,0},Table[0,2t+1]},t,"StatesGraphStructure",AspectRatio->3/2]]&/@
79
Out[]=

,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
