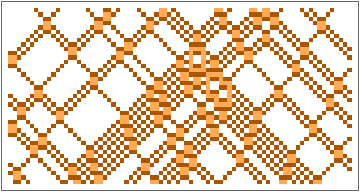
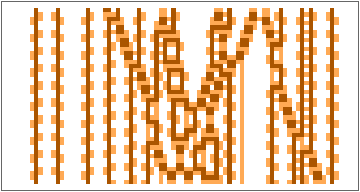
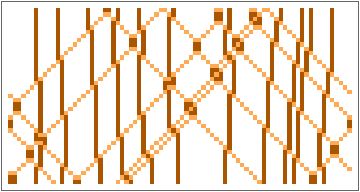
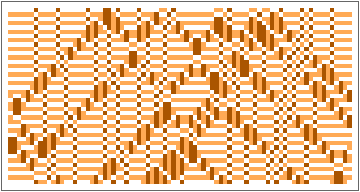
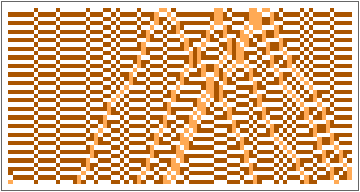
In[]:=
GraphicsRow[ArrayPlot[#,ColorRules->{0->White,1->Lighter[Orange],2->Darker[Orange]}]&/@Partition[ResourceFunction["BlockCellularAutomaton"][{{2,2}{1,1},{1,1}{2,2},{1,2}{1,2},{2,1}{2,1},{2,0}{0,2},{1,0}{1,0},{0,2}{2,0},{0,1}{0,1},{0,0}{0,0}},CenterArray[Table[2,21],80],1500],300],10]
Out[]=
In[]:=
ResourceFunction["BlockCellularAutomaton"][{{2,2}{1,1},{1,1}{2,2},{1,2}{1,2},{2,1}{2,1},{2,0}{0,2},{1,0}{1,0},{0,2}{2,0},{0,1}{0,1},{0,0}{0,0}},CenterArray[Table[2,21],80],200]//Last
Out[]=
{0,0,0,0,0,0,2,0,0,0,0,2,0,0,0,0,0,0,2,0,0,0,2,2,0,2,0,0,0,0,2,0,0,0,0,1,1,0,2,0,0,0,0,0,0,0,0,0,1,1,0,2,0,0,0,0,1,1,0,1,1,0,0,2,0,0,0,0,2,0,2,0,0,0,0,2,0,0,0,0}
In[]:=
ListLinePlot[%70]
Out[]=
In[]:=
ParityPairings[Tuples[Range[0,1],2]]
Out[]=
{{{{0,0},{0,1}},{{1,0},{1,1}}},{{{0,0},{1,0}},{{0,1},{1,1}}},{{{0,0},{1,1}},{{0,1},{1,0}}},{{{0,0},{0,0}},{{0,1},{0,1}},{{1,0},{1,1}}},{{{0,0},{0,0}},{{0,1},{1,0}},{{1,1},{1,1}}},{{{0,0},{0,0}},{{0,1},{1,1}},{{1,0},{1,0}}},{{{0,0},{0,1}},{{1,0},{1,0}},{{1,1},{1,1}}},{{{0,0},{1,0}},{{0,1},{0,1}},{{1,1},{1,1}}},{{{0,0},{1,1}},{{0,1},{0,1}},{{1,0},{1,0}}},{{{0,0},{0,0}},{{0,1},{0,1}},{{1,0},{1,0}},{{1,1},{1,1}}}}
In[]:=
symmetricQ[rules_]:=Sort[Map[Reverse,rules,{2}]]===Sort[rules]
In[]:=
allrules=Select[Rule@@@Union[Join[#,Reverse/@#]]&/@ParityPairings[Tuples[Range[0,2],2]],symmetricQ];
In[]:=
ResourceFunction["InteractiveListSelector"][(ArrayPlot[ResourceFunction["BlockCellularAutomaton"][#,{0,0,0,0,0,0,2,0,0,0,0,2,0,0,0,0,0,0,2,0,0,0,2,2,0,2,0,0,0,0,2,0,0,0,0,1,1,0,2,0,0,0,0,0,0,0,0,0,1,1,0,2,0,0,0,0,1,1,0,1,1,0,0,2,0,0,0,0,2,0,2,0,0,0,0,2,0,0,0,0},40],ColorRules->{0->White,1->Lighter[Orange],2->Darker[Orange]}]->#)&/@allrules]
Out[]=