In[]:=
Histogram[Table[Total[Take[ReplacePart[Table[0,200],Thread[RandomSample[Range[200],80]->1]],40]],10000]]
Out[]=

Glauber multiway system

Entropy spectrum; how many of each block occurs

Entropy[]
In[]:=
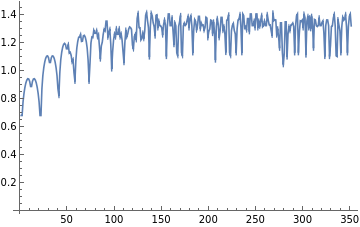
ListLinePlot[Entropy/@ResourceFunction["BlockCellularAutomaton"][{{2,2}{1,1},{1,1}{2,2},{1,2}{1,2},{2,1}{2,1},{2,0}{0,2},{1,0}{1,0},{0,2}{2,0},{0,1}{0,1},{0,0}{0,0}},CenterArray[Table[2,20],80],350]]
Out[]=
In[]:=
Table[ListLinePlot[Entropy[Partition[#,b,1]]&/@ResourceFunction["BlockCellularAutomaton"][{{2,2}{1,1},{1,1}{2,2},{1,2}{1,2},{2,1}{2,1},{2,0}{0,2},{1,0}{1,0},{0,2}{2,0},{0,1}{0,1},{0,0}{0,0}},CenterArray[Table[2,20],80],350]],{b,10}]
Out[]=

,
,
,
,
,
,
,
,
,

In[]:=
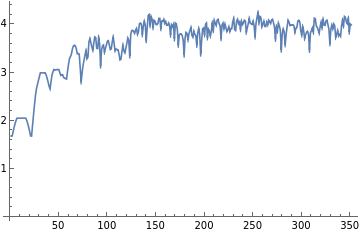
ListLinePlot[Entropy[Partition[#,10,1]]&/@ResourceFunction["BlockCellularAutomaton"][{{2,2}{1,1},{1,1}{2,2},{1,2}{1,2},{2,1}{2,1},{2,0}{0,2},{1,0}{1,0},{0,2}{2,0},{0,1}{0,1},{0,0}{0,0}},CenterArray[Table[2,20],80],1000]]
Out[]=
In[]:=
ListLinePlot[MaxBlob/@ResourceFunction["BlockCellularAutomaton"][{{2,2}{1,1},{1,1}{2,2},{1,2}{1,2},{2,1}{2,1},{2,0}{0,2},{1,0}{1,0},{0,2}{2,0},{0,1}{0,1},{0,0}{0,0}},CenterArray[Table[2,20],80],1000]]
Out[]=
In[]:=
ListLinePlot[Entropy[Partition[#,10,1]]&/@ResourceFunction["BlockCellularAutomaton"][{{2,2}{1,1},{1,1}{2,2},{1,2}{1,2},{2,1}{2,1},{2,0}{0,2},{1,0}{1,0},{0,2}{2,0},{0,1}{0,1},{0,0}{0,0}},CenterArray[Table[2,20],80],10000]]
Out[]=
In[]:=
ListLinePlot[Entropy[Partition[#,10,1]]&/@ResourceFunction["BlockCellularAutomaton"][{{2,2}{1,1},{1,1}{2,2},{1,2}{1,2},{2,1}{2,1},{2,0}{0,2},{1,0}{1,0},{0,2}{2,0},{0,1}{0,1},{0,0}{0,0}},CenterArray[Table[2,20],80],10000],PlotRange->All]
Out[]=
In[]:=
ListLinePlot[MaxBlob/@ResourceFunction["BlockCellularAutomaton"][{{2,2}{1,1},{1,1}{2,2},{1,2}{1,2},{2,1}{2,1},{2,0}{0,2},{1,0}{1,0},{0,2}{2,0},{0,1}{0,1},{0,0}{0,0}},CenterArray[Table[2,20],80],10000],PlotRange->All]
Out[]=
In[]:=
Table[ListLinePlot[Entropy[Partition[#,b,1]]&/@ResourceFunction["BlockCellularAutomaton"][{{2,2}{1,1},{1,1}{2,2},{1,2}{1,2},{2,1}{2,1},{2,0}{0,2},{1,0}{1,0},{0,2}{2,0},{0,1}{0,1},{0,0}{0,0}},RandomInteger[2,80],350]],{b,5,7}]
Out[]=

,
,

In[]:=
GraphicsRow[ArrayPlot[#,ColorRules->{0->White,1->Lighter[Orange],2->Darker[Orange]},ImageSize->{Automatic,330}]&/@Partition[ResourceFunction["BlockCellularAutomaton"][{{2,2}{1,1},{1,1}{2,2},{1,2}{1,2},{2,1}{2,1},{2,0}{0,2},{1,0}{1,0},{0,2}{2,0},{0,1}{0,1},{0,0}{0,0}},{0,0,0,1,0,0,0,0,2,0,0,0,1,2,0,0,0,0,1,2,1,0,0,1,0,0,0,2,0,1,0,1,0,0,1,0,0,0,0,0,1,2,0,1,1,1,0,0,0,2,0,0,0,0,0,2,0,0,0,2,0,2,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,2,1},50000],350,5000]]
Filter out periodic part...
Be able to figure out what survived for a while....

There are cycles that have readily visible structures that survive throughout the cycle....

“Local structure conservation law”
[ Probably in an infinite region, every structure is eventually destroyed, because there is a “nemesis” for every structure ]

Destruction of the checker flag.... etc.

A single isolated 1 cannot be destroyed.... [is this true?]
2 adjacent gives jig