Select cases with a particular number of particles
Select cases with a particular number of particles
In[]:=
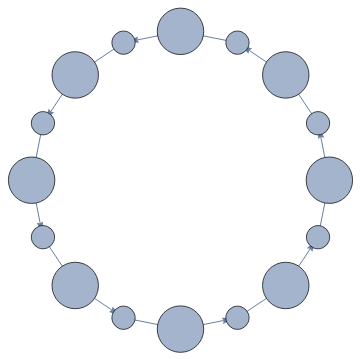
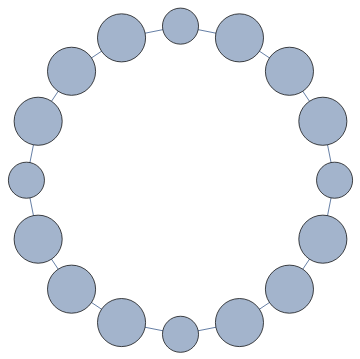
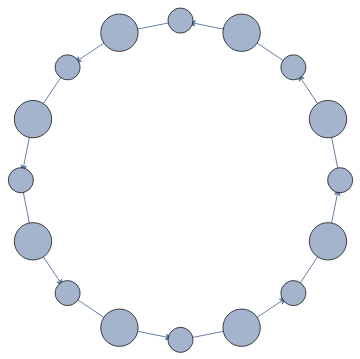
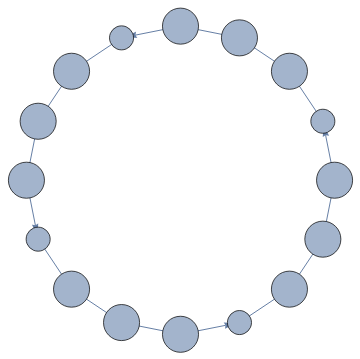
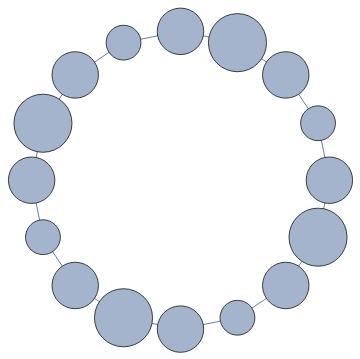
ggg=Graph[Flatten[Table[{#,i}->{Last[ResourceFunction["BlockCellularAutomaton"][{{2,2}{1,1},{1,1}{2,2},{1,2}{1,2},{2,1}{2,1},{2,0}{0,2},{1,0}{1,0},{0,2}{2,0},{0,1}{0,1},{0,0}{0,0}},#1,1,i]],1-i},{i,0,1}]&/@Select[Tuples[{0,1,2},8],Total[Sign[#]]==5&]],VertexSize->{x_:>.2MaxBlob[First@x]}]
Out[]=
In[]:=
Length[WeaklyConnectedGraphComponents[ggg]]
Out[]=
224
In[]:=
Select[Tuples[{0,1,2},8],Total[Sign[#]]==5&]//Length
Out[]=
1792
In[]:=
1792/16
Out[]=
112
Want to remove components related to others by rotation...
Want to remove components related to others by rotation...
In[]:=
Length/@GatherBy[{#,Sort[ResourceFunction["CanonicalListRotation"][First[#]]&/@VertexList[#]]}&/@WeaklyConnectedGraphComponents[ggg],Last]
Out[]=
{2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,2,2,2,1,2,1,2,2,2,2,2,2,2,1,2,2,2,2,2,2,2,2,2,1,2,2,1,2,2,2,2,2,2,2,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,2,1,1,2,2,2,2,2,2,2,1,2,2,2,2,2,2,1,2,2,2,2,2,2,1,1,2,2,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,2,1,2,2,1,2,1,1,1,1,2,1,1}
In[]:=
GraphUnion[#[[1,1]]&/@GatherBy[{#,Sort[ResourceFunction["CanonicalListRotation"][First[#]]&/@VertexList[#]]}&/@WeaklyConnectedGraphComponents[ggg],Last]]
,
,
,
,
,
,
,
,
,
,114.
Out[]=
GraphUnion
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
In[]:=
GraphUnion@@(#[[1,1]]&/@GatherBy[{#,Sort[ResourceFunction["CanonicalListRotation"][First[#]]&/@VertexList[#]]}&/@WeaklyConnectedGraphComponents[ggg],Last])
Out[]=
Cycle Sizes for Simple vs. Random States [WRONG!]
Cycle Sizes for Simple vs. Random States [WRONG!]
NKS code
NKS code
“Simple” initial condition is a single large blob [[[ we know there is a particular cycle that has the large blob case ; as well as its cyclic friends ]]]
Only one of these is left-right symmetric
Some of the longest lived are actually the most regular.....
Use weighted randomness, etc.
Size 30 random inits
Size 30 random inits
Majority of randomly chosen states are on short cycles....
[[ Can we predict period from e.g. particle count? ]]
Size 80, 50, etc.
Size 80, 50, etc.