Entropy Estimate

In[]:=
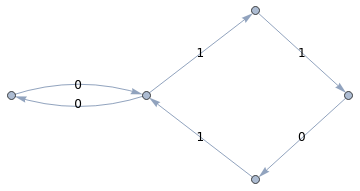
g=Graph[{DirectedEdge[a,b,0],DirectedEdge[b,a,0],DirectedEdge[a,c,1],DirectedEdge[c,d,1],DirectedEdge[d,e,0],DirectedEdge[e,a,1]},EdgeLabels"EdgeTag",EdgeLabelStyle12,EdgeStyleOpacity[0.5],AspectRatio1/2]
Out[]=
In[]:=
AdjacencyMatrix[Graph[{DirectedEdge[a,b,0],DirectedEdge[b,a,0],DirectedEdge[a,c,1],DirectedEdge[c,d,1],DirectedEdge[d,e,0],DirectedEdge[e,a,1]},EdgeLabels"EdgeTag",EdgeLabelStyle12,EdgeStyleOpacity[0.5],AspectRatio1/2]]//Normal
Out[]=
{{0,1,1,0,0},{1,0,0,0,0},{0,0,0,1,0},{0,0,0,0,1},{1,0,0,0,0}}
In[]:=
Table[Total[Flatten[MatrixPower[{{0,1,1,0,0},{1,0,0,0,0},{0,0,0,1,0},{0,0,0,0,1},{1,0,0,0,0}},t]]],{t,20}]
Out[]=
{6,8,10,13,16,21,26,34,42,55,68,89,110,144,178,233,288,377,466,610}
In[]:=
Ratios[%]//N
Out[]=
{1.33333,1.25,1.3,1.23077,1.3125,1.2381,1.30769,1.23529,1.30952,1.23636,1.30882,1.23596,1.30909,1.23611,1.30899,1.23605,1.30903,1.23607,1.30901}
In[]:=
FindSequenceFunction[{6,8,10,13,16,21,26,34,42,55,68,89,110,144,178,233,288,377,466,610},t]
Out[]=
1
5(2+
5
)(9+4
5
)
-
5
2
-
t
2
2
15
t
(-)
2
t/2
(-1+
5
)
+15
t

2
t/2
(-1+
5
)
+7
t
(-)
10
t/2
(-1+
5
)
+7
t

10
t/2
(-1+
5
)
-50
t
(-)
t/2
(-1+
5
)
1+
5
+50
t

t/2
(-1+
5
)
1+
5
+4560
-
1
2
+
t
2
(1+
5
)
-4560
t
(-1)
-
1
2
+
t
2
(1+
5
)
+2040
5
-
1
2
+
t
2
(1+
5
)
-2040
t
(-1)
5
-
1
2
+
t
2
(1+
5
)
+15
2(-1+
5
)
-
1
2
+
t
2
(1+
5
)
-15
t
(-1)
2(-1+
5
)
-
1
2
+
t
2
(1+
5
)
+7
10(-1+
5
)
-
1
2
+
t
2
(1+
5
)
-7
t
(-1)
10(-1+
5
)
-
1
2
+
t
2
(1+
5
)
+(1885-10)
2
t/2
(1+
5
)
+(1885+10)
t
(-1)
2
t/2
(1+
5
)
+(843-4)
10
t/2
(1+
5
)
+(843+4)
t
(-1)
10
t/2
(1+
5
)
+50
-1+
5
t/2
(1+
5
)
-50
t
(-1)
-1+
5
t/2
(1+
5
)
+22
5(-1+
5
)
t/2
(1+
5
)
-22
t
(-1)
5(-1+
5
)
t/2
(1+
5
)
-22
t
(-)
t/2
(-1+
5
)
5(1+
5
)
+22
t

t/2
(-1+
5
)
5(1+
5
)
In[]:=
FullSimplify[%]
Out[]=
1
5
1+
5
1
2
(-3-t)
2
-
1
2
πt

2
t/2
(-1+
5
)
2(-5+2
5
)+
-190+85
5
+
t/2
(1+
5
)
30+14
5
+
1990+890
5

πt
2

+2
t/2
(-1+
5
)
10-4
5
+
-190+85
5

πt

+
t/2
(1+
5
)
-30-14
5
+
1990+890
5

3πt
2

In[]:=
FindLinearRecurrence[{6,8,10,13,16,21,26,34,42,55,68,89,110,144,178,233,288,377,466,610}]
Out[]=
{0,1,0,1}
In[]:=
probs=(Counts[#]/Length[#])&/@GatherBy[If[MemberQ[#,DirectedEdge,Infinity,HeadsTrue],Nothing,#]&/@(Table[DirectedEdge[#[[n]],#[[n+1]]],{n,Length[#]-1}]&/@Module[{paths=Catenate[FindPath[g,First[#],Last[#],Infinity,All]&/@Join[Subsets[{a,b,c,d,e},{2}],Reverse/@Subsets[{a,b,c,d,e},{2}]]],cycles=Catenate[Table[RotateLeft[#,Length[#]-n],{n,Length[#]}]&/@(DeleteDuplicates/@Map[Delete[#,{{0},{3}}]&,FindCycle[g,Infinity,All],{2}])],newpaths},​​cycles=AssociationMap[With[{cont=Last[#]},RotateLeft[#,1]&/@Select[cycles,First[#]===cont&]]&,cycles];​​cycles=If[Length[#]<4,Join[#,Drop[#,1]],#]&/@Flatten[Table[With[{path=#},Table[Catenate[{path,Take[#,i]}],{i,Range[Length[#]]}]&/@(Take[#,UpTo[5-Length[path]]]&/@cycles[path])]&[Keys[cycles][[n]]],{n,Range[Length[cycles]]}],2];​​paths=DeleteDuplicates[Catenate[{paths,cycles}]];​​newpaths=AssociationMap[With[{cont=Last[#]},RotateLeft[#,1]&/@Select[cycles,First[#]===cont&]]&,paths];​​DeleteDuplicates[Join[paths,Flatten[Table[With[{path=#},Table[Catenate[{path,Take[#,i]}],{i,Range[Length[#]]}]&/@(Take[#,UpTo[5-Length[path]]]&/@newpaths[path])]&[paths[[n]]],{n,Range[Length[paths]]}],2]]]]/.((DirectedEdge@@Take[#,2]Last[#])&/@({Delete[#,0]}&/@EdgeList[g]))),Length]
Out[]=
{0}
1
2
,{1}
1
2
,{1,1}
1
4
,{0,1}
1
4
,{1,0}
1
4
,{0,0}
1
4
,{1,1,0}
1
10
,{0,1,1}
1
5
,{1,0,1}
1
10
,{0,1,0}
1
10
,{1,1,1}
1
10
,{0,0,0}
1
5
,{0,0,1}
1
10
,{1,0,0}
1
10
,{0,1,1,0}
1
13
,{1,0,1,0}
1
13
,{0,0,0,0}
2
13
,{1,1,1,0}
1
13
,{0,1,1,1}
1
13
,{1,0,1,1}
1
13
,{1,1,0,1}
1
13
,{0,0,1,1}
1
13
,{0,1,0,0}
1
13
,{1,0,0,0}
1
13
,{1,0,0,1}
1
13
,{0,0,0,1}
1
13

In[]:=
seq0=TSDirectEvolveSequence[PuffOut[IntegerDigits[506,2,9]],24552];
In[]:=
seq=Take[seq0,{100,-100}];
In[]:=
Table[SequenceCount[seq,#]&/@Tuples[{0,1},n],{n,5}]
Out[]=
{{36753,36741},{12253,17282,17283,12247},{6080,5036,5035,12247,5036,12246,12247,7211},{4052,2741,0,5036,5035,0,5036,7211,2741,2295,5035,7211,0,12246,7211,0},{2979,2741,0,2741,0,0,5036,0,2741,2294,0,0,0,5036,4049,0,2741,0,0,2295,5035,0,0,4049,0,0,5035,4049,0,4048,0,0}}
In[]:=
Entropy[2,#]&/@%
Out[]=
1,2,
5
2
,4+
1
16
-14-
3Log[3]
Log[2]
,5+
1
32
-12-
3Log[3]
Log[2]
-
17Log[17]
Log[2]

In[]:=
N[%]
Out[]=
{1.,2.,2.5,2.82782,2.30495}
In[]:=
Entropy[seq]//N
Out[]=
0.693147
In[]:=
2^%346
Out[]=
1.61681
In[]:=
RootApproximant[2^%]
Out[]=
1.62
…
In[]:=
Table[Length[Union[Partition[seq,n,1]]],{n,10}]
Out[]=
{2,4,8,12,15,20,25,33,41,53}
In[]:=
Table[Length[Union[Partition[seq,n,1]]],{n,14}]
Out[]=
{2,4,8,12,15,20,25,33,41,53,65,83,101,128}
In[]:=
FindSequenceFunction[{2,4,8,12,15,20,25,33,41,53,65,83,101,128},t]
Out[]=
FindSequenceFunction[{2,4,8,12,15,20,25,33,41,53,65,83,101,128},t]
In[]:=
Table[2^n-Length[Union[Partition[seq,n,1]]],{n,14}]
Out[]=
{0,0,0,4,17,44,103,223,471,971,1983,4013,8091,16256}
In[]:=
Log[2,%]//N
Out[]=
{1.,2.,3.,3.58496,3.90689,4.32193,4.64386,5.04439,5.35755,5.72792,6.02237,6.37504,6.65821,7.}
In[]:=
%/Range[Length[%]]
Out[]=
{1.,1.,1.,0.896241,0.781378,0.720321,0.663408,0.630549,0.595284,0.572792,0.547488,0.531253,0.51217,0.5}
In[]:=
ListStepPlot[%]
Out[]=
2
4
6
8
10
12
14
0.2
0.4
0.6
0.8
1.0
In[]:=
Ratios[{2,4,8,12,15,20,25,33,41,53,65,83,101,128}]//N
Out[]=
{2.,2.,1.5,1.25,1.33333,1.25,1.32,1.24242,1.29268,1.22642,1.27692,1.21687,1.26733}
In[]:=
ListStepPlot[%]
final state | cycle length |
27:....
10 X 54:1401...

Mano’s Calculation

More

Cyclic Tag

Odds and Ends

Backwards Evolution

Riemann Hypothesis

Iterative version

Causal Graph

Histograms

General Tag Computations

Entropy

m-grams