Growth rate of geodesic balls ... AKA how many numbers can one reach after t steps?
Growth rate of geodesic balls ... AKA how many numbers can one reach after t steps?
Given that we allow multiplicands up to s, what is the number of numbers reached before t steps?
Given that we allow multiplicands up to s, what is the number of numbers reached before t steps?
The following asks how to make numbers from things smaller than them:
The following asks how to make numbers from things smaller than them:
In[]:=
MultiplicativeParts[n_]:=Flatten[Table[##]&@@@FactorInteger[n]]
In[]:=
AllMultiplierDecompositions[n_]:=Union[With[{m=MultiplicativeParts[n]},Catenate[Function[u,(Times@@@TakeList[u,#])&/@Catenate[Permutations/@IntegerPartitions[Length[m]]]]/@Permutations[m]]]]
In[]:=
AllMultiplierDecompositions[12]
Out[]=
{{12},{2,6},{3,4},{4,3},{6,2},{2,2,3},{2,3,2},{3,2,2}}
In[]:=
With[{max=40},Grid[Prepend[Transpose[Normal[SparseArray[Flatten[Table[Normal[KeyMap[{n,#}&,KeySort[Counts[Length/@AllMultiplierDecompositions[n]]]]],{n,max}]],Automatic,""]]],Range[max]],Frame->All,Background->{Automatic,{LightBlue,{None}}}]]
Out[]=
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
1 | 2 | 2 | 1 | 2 | 4 | 2 | 2 | 3 | 4 | 4 | 2 | 2 | 6 | 1 | 2 | 2 | 4 | 6 | 4 | 2 | 2 | 2 | 7 | 2 | 2 | 6 | |||||||||||||
1 | 3 | 3 | 3 | 3 | 9 | 1 | 3 | 6 | 6 | 12 | 9 | ||||||||||||||||||||||||||||
1 | 4 | 4 | 6 | 4 | |||||||||||||||||||||||||||||||||||
1 |
What this shows is how frequently the number will show up at a given step number (i.e. its path weight at that step number)
Prime will only show up after 1 step
Prime powers p^m will show up with a 1 at step m Binomial[m,t]
Prime will only show up after 1 step
Prime powers p^m will show up with a 1 at step m Binomial[m,t]
Prime powers p^m will show up with a 1 at step m Binomial[m,t]
2nd row: is it number of times the number shows up in a 2D grid smaller than itself
2nd row: is it number of times the number shows up in a 2D grid smaller than itself
E.g. for 20:
In[]:=
Count[Flatten[Table[ij,{i,19},{j,19}]],20]
Out[]=
4
In[]:=
Table[Count[Flatten[Table[ij,{i,n-1},{j,n-1}]],n],{n,30}]
Out[]=
{0,0,0,1,0,2,0,2,1,2,0,4,0,2,2,3,0,4,0,4,2,2,0,6,1,2,2,4,0,6}
Number of ways to form the number out of pairs of numbers.....
In[]:=
Grid[Table[ij,{i,11},{j,11}]/.12->Item[12,Background->LightRed]]
Out[]=
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 |
3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 |
4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 |
5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 |
6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 |
7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 |
8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 |
9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 |
10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 |
11 | 22 | 33 | 44 | 55 | 66 | 77 | 88 | 99 | 110 | 121 |
Doesn’t work for cube....
In[]:=
Count[Flatten[Table[ijk,{i,19},{j,19},{k,19}]],20]
Out[]=
15
Total number of numbers reached after 1, 2, 3 ... steps given
Total number of numbers reached after 1, 2, 3 ... steps given
In[]:=
gg=Table[Last[ResourceFunction["GraphNeighborhoodVolumes"][With[{m=k},NestGraph[n|->Table[an,{a,m}],1,10]],{1}]],{k,2,13}]
Out[]=
{{1,2,3,4,5,6,7,8,9,10,11},{1,3,6,10,15,21,28,36,45,55,66},{1,4,9,16,25,36,49,64,81,100,121},{1,5,14,30,55,91,140,204,285,385,506},{1,6,18,40,75,126,196,288,405,550,726},{1,7,25,65,140,266,462,750,1155,1705,2431},{1,8,30,80,175,336,588,960,1485,2200,3146},{1,9,36,100,225,441,784,1296,2025,3025,4356},{1,10,42,120,275,546,980,1632,2565,3850,5566},{1,11,53,173,448,994,1974,3606,6171,10021,15587},{1,12,59,194,504,1120,2226,4068,6963,11308,17589},{1,13,72,266,770,1890,4116,8184,15147,26455,44044}}
In[]:=
ff=Table[LinearRecurrence[Table[(-1)^(k+1)Binomial[PrimePi[m]+1,k],{k,1,PrimePi[m]+1}],Prepend[Length/@NestList[Union[Times@@#&/@Tuples[{Range[m],#}]]&,Range[m],PrimePi[m]-1],1],11],{m,2,13}]
Out[]=
{{1,2,3,4,5,6,7,8,9,10,11},{1,3,6,10,15,21,28,36,45,55,66},{1,4,9,16,25,36,49,64,81,100,121},{1,5,14,30,55,91,140,204,285,385,506},{1,6,18,40,75,126,196,288,405,550,726},{1,7,25,65,140,266,462,750,1155,1705,2431},{1,8,30,80,175,336,588,960,1485,2200,3146},{1,9,36,100,225,441,784,1296,2025,3025,4356},{1,10,42,120,275,546,980,1632,2565,3850,5566},{1,11,53,173,448,994,1974,3606,6171,10021,15587},{1,12,59,194,504,1120,2226,4068,6963,11308,17589},{1,13,72,266,770,1890,4116,8184,15147,26455,44044}}
In[]:=
Grid[ff,Frame->All,AlignmentRight]
Out[]=
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
1 | 3 | 6 | 10 | 15 | 21 | 28 | 36 | 45 | 55 | 66 |
1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 | 121 |
1 | 5 | 14 | 30 | 55 | 91 | 140 | 204 | 285 | 385 | 506 |
1 | 6 | 18 | 40 | 75 | 126 | 196 | 288 | 405 | 550 | 726 |
1 | 7 | 25 | 65 | 140 | 266 | 462 | 750 | 1155 | 1705 | 2431 |
1 | 8 | 30 | 80 | 175 | 336 | 588 | 960 | 1485 | 2200 | 3146 |
1 | 9 | 36 | 100 | 225 | 441 | 784 | 1296 | 2025 | 3025 | 4356 |
1 | 10 | 42 | 120 | 275 | 546 | 980 | 1632 | 2565 | 3850 | 5566 |
1 | 11 | 53 | 173 | 448 | 994 | 1974 | 3606 | 6171 | 10021 | 15587 |
1 | 12 | 59 | 194 | 504 | 1120 | 2226 | 4068 | 6963 | 11308 | 17589 |
1 | 13 | 72 | 266 | 770 | 1890 | 4116 | 8184 | 15147 | 26455 | 44044 |
s across the top ... t down
The sth column is the dimension s multiplication table
In[]:=
Differences/@ff
Out[]=
{{1,1,1,1,1,1,1,1,1,1},{2,3,4,5,6,7,8,9,10,11},{3,5,7,9,11,13,15,17,19,21},{4,9,16,25,36,49,64,81,100,121},{5,12,22,35,51,70,92,117,145,176},{6,18,40,75,126,196,288,405,550,726},{7,22,50,95,161,252,372,525,715,946},{8,27,64,125,216,343,512,729,1000,1331},{9,32,78,155,271,434,652,933,1285,1716},{10,42,120,275,546,980,1632,2565,3850,5566},{11,47,135,310,616,1106,1842,2895,4345,6281},{12,59,194,504,1120,2226,4068,6963,11308,17589}}
Number of multiplicands across the top; number of steps down
In[]:=
Grid[%,Frame->All,AlignmentRight]
Out[]=
1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 |
4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 | 121 |
5 | 12 | 22 | 35 | 51 | 70 | 92 | 117 | 145 | 176 |
6 | 18 | 40 | 75 | 126 | 196 | 288 | 405 | 550 | 726 |
7 | 22 | 50 | 95 | 161 | 252 | 372 | 525 | 715 | 946 |
8 | 27 | 64 | 125 | 216 | 343 | 512 | 729 | 1000 | 1331 |
9 | 32 | 78 | 155 | 271 | 434 | 652 | 933 | 1285 | 1716 |
10 | 42 | 120 | 275 | 546 | 980 | 1632 | 2565 | 3850 | 5566 |
11 | 47 | 135 | 310 | 616 | 1106 | 1842 | 2895 | 4345 | 6281 |
12 | 59 | 194 | 504 | 1120 | 2226 | 4068 | 6963 | 11308 | 17589 |
In[]:=
Table[Binomial[n,3],{n,10}]
Out[]=
{0,0,1,4,10,20,35,56,84,120}
Number of numbers that appear exactly at a given row...
In[]:=
Graph[ResourceFunction["NestGraphTagged"][n|->{2n,3n},1,10,"StateLabeling"->True,"RuleStyling"->None],GraphLayout"LayeredDigraphEmbedding",AspectRatio1/2]
Out[]=
In[]:=
Graph[ResourceFunction["NestGraphTagged"][n|->{n,2n,3n},1,10,"StateLabeling"->True,"RuleStyling"->None],GraphLayout"LayeredDigraphEmbedding",AspectRatio1/2]
Out[]=
In[]:=
Graph3D[ResourceFunction["NestGraphTagged"][n|->{2n,3n,4n},1,6,"StateLabeling"->True,"RuleStyling"->None]]
Out[]=
After 2 steps, one gets the distinct numbers in the s×s multiplication table:
After 2 steps, one gets the distinct numbers in the s×s multiplication table:
[ “numbers of low multiplicative complexity” ]
[ “numbers of low multiplicative complexity” ]
When a number can be generated in more ways, it adds an edge in the graph, but what matters to the geodesic volume is the first appearance of each number....
How many distinct numbers appear? [Given s and t, how long will be list be?] In the “free” case with no merging, there will be s^t such numbers. But many can be generated in multiple ways, and some can’t be generated
How many distinct numbers appear? [Given s and t, how long will be list be?] In the “free” case with no merging, there will be s^t such numbers. But many can be generated in multiple ways, and some can’t be generated
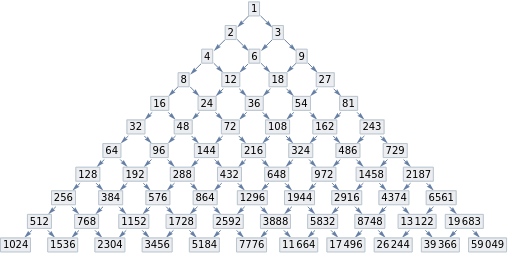
With 1 multiplier, just get powers of 2.
With 2 multipliers [[ volume of ball is triangular numbers ]]
3 multipliers
[[ volume of ball is the squares ]]
4 multipliers
[ Squares ]
When Does a Number First Occur?
When Does a Number First Occur?
Any given number
As a function of s, how fast does the ball grow in t?
As a function of s, how fast does the ball grow in t?
As a function of s, the exponent of t is PrimePi[s]
The fastest way to generate numbers is by combining primes......
At each step, you pick one of the q available numbers.... t^q
Branchial Graphs
Branchial Graphs
Each edge could be labeled by the common ancestor that led to it..... [[[[ Ed: need to actually label them ]]]]
Stacked Plot
Stacked Plot
Rulial Space
Rulial Space
Making a square
Making a square
Linear Recurrences
Linear Recurrences