Bottom Up Approach
Bottom Up Approach
Start with phase space of possible states; add rules (either through homotopy or other ways)
Top Down Approach
Top Down Approach
Start from the everything object
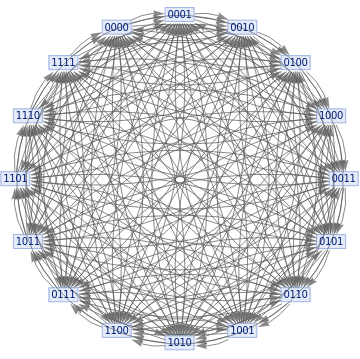
Is it just a complete graph?
The nodes are roughly the states of the system
The tokens within the states can have a more complicated relationship
Relations on rulial multiway graph
Relations on rulial multiway graph
For all states X and Y (that are representable in this computational model) there is a rule that goes from X to Y and Y to X
In[]:=
Graph[Flatten@Outer[DirectedEdge,Tuples[{1,0},4],Tuples[{1,0},4],1]]
Out[]=
In[]:=
SimpleGraph[Graph[Flatten@Outer[DirectedEdge,Tuples[{1,0},4],Tuples[{1,0},4],1]]]
Out[]=
Example of dynamics: just flip any possible bit
Different case: overlaps:
In[]:=
DeBruijnGraph[4,2]
Out[]=
In[]:=
ResourceFunction["MultiwaySystem"][{{0}->{1},{1}->{0}},{{0,0,0,0}},3,"StatesGraph"]
Out[]=
In[]:=
ResourceFunction["MultiwaySystem"][{{0}->{1},{1}->{0}},{{0,0,0,0}},6,"StatesGraph"]
Out[]=
Have to add rules somehow (e.g. through completion or directly through transitive closure + reversal + reflexivity [self loops])
In[]:=
TransitiveClosureGraph[ResourceFunction["MultiwaySystem"][{{0}->{1},{1}->{0}},{{0,0,0,0}},6,"StatesGraph"]]
Out[]=
In[]:=
ResourceFunction["MultiwaySystem"][{{0}->{1},{1}->{0}},{{0,0,0,0}},6,"EvolutionEventsGraph"]
Out[]=
TEG is the most shattered
Glocal multiway shatters states but not events
Glocal multiway shatters states but not events
The rule 0↔1 + transitive closure is an alternative to the {any list}{any list}
The rule 0↔1 + transitive closure is an alternative to the {any list}{any list}
This is the states graph... we could imagine forming it progressively from a multiway evolution
In a top down approach the only obvious constraints are that the states and causal partial orders are compatible....
In a top down approach the only obvious constraints are that the states and causal partial orders are compatible....
Imagine a generalized Turing machine which modifies blocks....
Imagine a generalized Turing machine which modifies blocks....
E.g. a string substitution system with “spectator” characters ... which are accounted for in causal relations but aren’t involved in the state transitions
E.g. a string substitution system with “spectator” characters ... which are accounted for in causal relations but aren’t involved in the state transitions
General Picture
General Picture
“Generate all possible states” is a computation
“Generate all possible states” is a computation
Completions add cross-bracing ...
Completions add cross-bracing ...
Sometimes the completions don’t have infinite consequences
Either because it goes to a normal form... or it has only a finite number of states or ......
[Decidability]
Either because it goes to a normal form... or it has only a finite number of states or ......
[Decidability]
For a decidable theory, the set of completion is always finite [e.g. group theory]
For a decidable theory, the set of completion is always finite [e.g. group theory]
There is an “optimally unravelled” axiom system for group theory...
What is the minimal completion of e.g. Boolean algebra?
This would allow all proofs to be done with pure substitution....
This would allow all proofs to be done with pure substitution....