Slicing the ruliad differently

These are possible sets of axioms to assume:

In[]:=
Flatten[ResourceFunction["EnumerateSubstitutionSystemRules"][{Rule@@#},1]&/@Union[Sort/@Catenate[Table[{i,j},{i,1,4},{j,1,4}]]]]/.Rule->TwoWayRule
Out[]=
{AA,AAA,AAAA,AAAAA,AAAA,AAAAA,AAAAAA,AAAAAA,AAAAAAA,AAAAAAAA}
Given these rules, this is what happens after a single step:
In[]:=
VertexList[ResourceFunction["TokenEventGraph"][{{r1_,r2_}:>StringApply[r1,r2]},{#},1,"TokenMultiplicity"->Automatic,"EventDeduplication"->True,"TokenLabeling"->False],_TwoWayRule]&/@%
Out[]=
{{AA},{AAA,AA,AAAA,AAAA},{AAAA,AA,AAAAAA,AAAAAA},{AAAAA,AA,AAAAAAAA,AAAAAAAA},{AAAA},{AAAAA,AAAA,AAAAAA,AAAAAA},{AAAAAA,AAAA,AAAAAAAA,AAAAAAAA},{AAAAAA},{AAAAAAA,AAAAAA,AAAAAAAA,AAAAAAAA},{AAAAAAAA}}
In[]:=
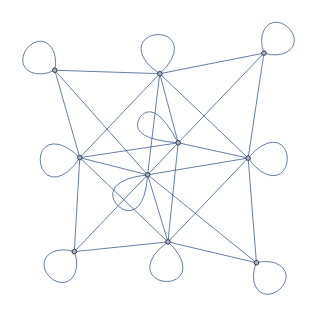
RelationGraph[IntersectingQ,%]
Out[]=
In[]:=
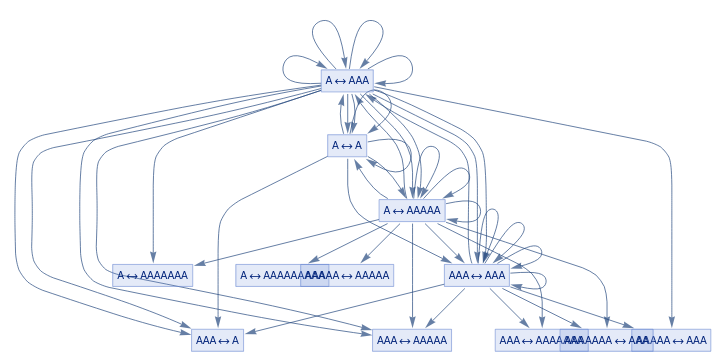
ResourceFunction["TokenEventGraph"][{{r1_,r2_}:>StringApply[r1,r2]},{"A""AAA","A""A","A""AAAAA","AAA""AAA"},1,"TokenMultiplicity"->Automatic,"EventDeduplication"->True,"TokenLabeling"->True,GraphLayout->{"LayeredDigraphEmbedding","RootVertex"->{"A""AAA","A""A","A""AAAAA","AAA""AAA"}}]
Out[]=
In[]:=
removeEvents[ResourceFunction["TokenEventGraph"][{{r1_,r2_}:>StringApply[r1,r2]},{"A""AAA","A""A","A""AAAAA","AAA""AAA"},1,"TokenMultiplicity"->Automatic,"EventDeduplication"->True,"TokenLabeling"->True,GraphLayout->{"LayeredDigraphEmbedding","RootVertex"->{"A""AAA","A""A","A""AAAAA","AAA""AAA"}}]]
Out[]=
In[]:=
removeEvents[ResourceFunction["TokenEventGraph"][{{r1_,r2_}:>StringApply[r1,r2]},{"A""AA"},1,"TokenMultiplicity"->Automatic,"EventDeduplication"->True,"TokenLabeling"->True]]
Out[]=
In[]:=
removeEvents[ResourceFunction["TokenEventGraph"][{{r1_,r2_}:>StringApply[r1,r2]},{"A""AA"},2,"TokenMultiplicity"->Automatic,"EventDeduplication"->True,"TokenLabeling"->True,GraphLayout->{"LayeredDigraphEmbedding","RootVertex"->{"A""AA"}}]]
Out[]=
In[]:=
removeEvents[ResourceFunction["TokenEventGraph"][{{r1_,r2_}:>StringApply[r1,r2]},{"A""AA"},3,"TokenMultiplicity"->Automatic,"EventDeduplication"->True,"TokenLabeling"->False,GraphLayout->{"LayeredDigraphEmbedding","RootVertex"->{"A""AA"}},AspectRatio->1/2]]
Out[]=

Largely incompatible entailment cones:

This object is the overlaps of the entailment codes of all possible choices of axiom systems

This is similar to a slice of the causal graph (? to the branchial graph) representing an instantaneous state of metamathematics

This separately renders edges from different cones

This is showing how multiple “shallow cones” knit together

This is like a branchial graph except that we explicitly show the ancestors

The observer has a thickened view of what molecules exist...