In[]:=
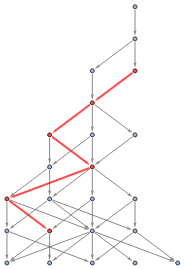
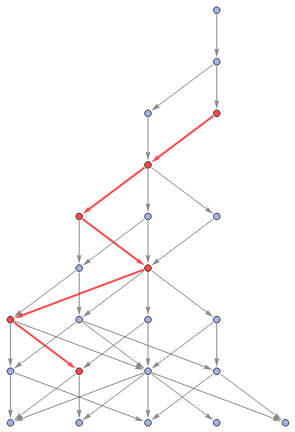
With[{g=Graph[ResourceFunction["MultiwaySystem"][{"A"->"BBB","BB"->"A"},"A",8,"StatesGraph"],AspectRatio->1.5]},HighlightGraph[g,Style[PathGraph[FindShortestPath[g,"BA","AAB"],DirectedEdgesTrue],Red,Thick]]]
Out[]=
In[]:=
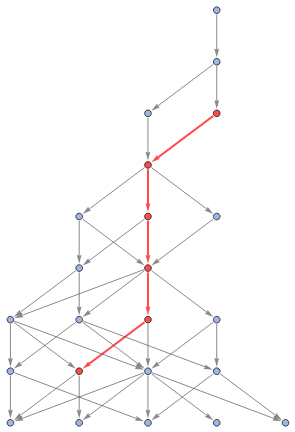
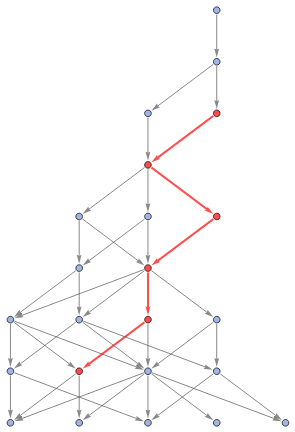
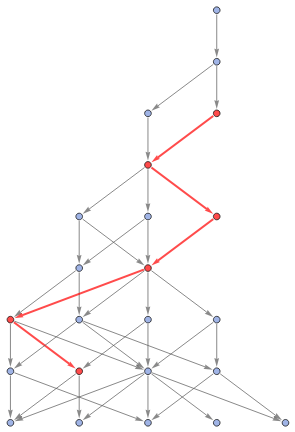
With[{g=Graph[ResourceFunction["MultiwaySystem"][{"A"->"BBB","BB"->"A"},"A",8,"StatesGraphStructure"],AspectRatio->1.5]},HighlightGraph[g,Style[PathGraph[#,DirectedEdgesTrue],Red,Thick]]&/@FindPath[g,"BA","AAB",All,3]]
Out[]=
,
,
Are the paths homotopically deformable into each other?
Are the paths homotopically deformable into each other?
In[]:=
With[{g=Graph[ResourceFunction["MultiwaySystem"][{"A"->"BBB","BB"->"A"},"A",8,"StatesGraphStructure"],AspectRatio->1.5]},HighlightGraph[g,Style[PathGraph[#,DirectedEdgesTrue],Red,Thick]]&/@FindPath[g,"BA","AAB",All,All]]
Out[]=
,
,
,
,
,
,
,
In[]:=
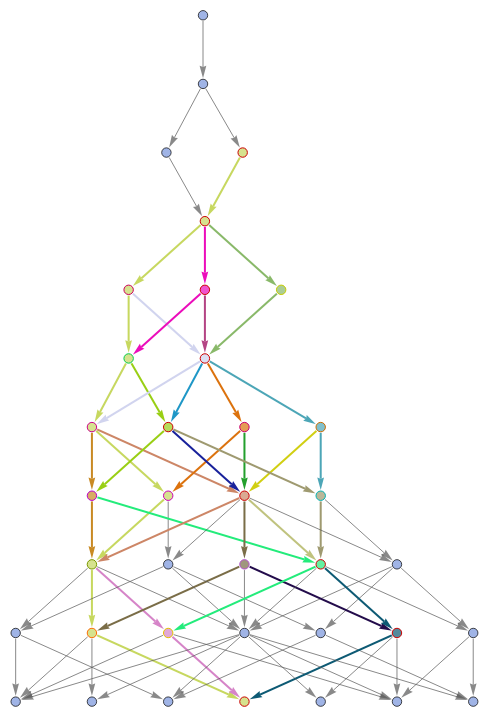
With[{g=Graph[ResourceFunction["MultiwaySystem"][{"A"->"BBB","BB"->"A"},"A",8,"StatesGraphStructure"],AspectRatio->1.5]},HighlightGraph[g,Style[PathGraph[#,DirectedEdgesTrue],RandomColor[],Thick]&/@FindPath[g,"BA","AAB",All,All]]]
Out[]=
The presence of a hole is like a robust metamathematical statement
The presence of a hole is like a robust metamathematical statement
In[]:=
ResourceFunction["MultiwaySystem"][{"A"->"BBB","BB"->"A"},"A",10,"StatesGraphStructure"]//VertexList
Out[]=
{A,BBB,AB,BA,BBBB,ABB,BAB,BBA,AA,BBBBB,ABBB,BABB,BBAB,BBBA,AAB,ABA,BAA,BBBBBB,ABBBB,BABBB,BBABB,BBBAB,BBBBA,AABB,ABAB,ABBA,BAAB,BABA,BBAA,BBBBBBB,AAA,ABBBBB,BABBBB,BBABBB,BBBABB,BBBBAB,BBBBBA}
In[]:=
With[{g=Graph[ResourceFunction["MultiwaySystem"][{"A"->"BBB","BB"->"A"},"A",10,"StatesGraphStructure"],AspectRatio->1.5]},HighlightGraph[g,Style[PathGraph[#,DirectedEdgesTrue],RandomColor[],Thick]&/@FindPath[g,"BA","AAA",All,All]]]
Out[]=
E.g. Christopher’s sliding block example:
Towers of Hanoi analog [2020/Multiway-Games-05]
Towers of Hanoi analog [2020/Multiway-Games-05]
[[[ Something is wrong with moves here ... ]]]
String example
String example
I.e. there is confluence but it takes a while....
Examples with holes: https://www.wolframphysics.org/technical-introduction/the-updating-process-for-string-substitution-systems/testing-for-causal-invariance/#p-222
Examples with holes: https://www.wolframphysics.org/technical-introduction/the-updating-process-for-string-substitution-systems/testing-for-causal-invariance/#p-222
Adding a completion:
Claim: different disjoint regions of metamathematical space lead to the same result
Claim: different disjoint regions of metamathematical space lead to the same result
Disjoint axiom system sets can lead to the same theorems
If you admit the axioms from the different sides of the hole in metamathematical space then will this lead to an explosion...
If you admit the axioms from the different sides of the hole in metamathematical space then will this lead to an explosion...
We know it leads to a particular theorem being established .... but will it lead to an explosion of other theorems?
Is the bridging axiom paramathematical?
Is the bridging axiom paramathematical?
Bizarre new idea that bridges different areas....
When you see two different proofs of the same thing ... it’s basically showing a math problem : how do you get from one to the other?
When you see two different proofs of the same thing ... it’s basically showing a math problem : how do you get from one to the other?
Game analogy
Game analogy
Two different “cooperating” players : they go down disjoint paths : so they don’t understand each other’s strategies
[if the paths are continuously deformable then they can back each other up]
If two Towers of Hanoi players are solving the puzzle the same way ... they can learn from each other’s “microrecursions”
[if the paths are continuously deformable then they can back each other up]
If two Towers of Hanoi players are solving the puzzle the same way ... they can learn from each other’s “microrecursions”
Metamathematics
Metamathematics
If you go down different sides of the hole, there will not be agreement about objective reality of metamathematics