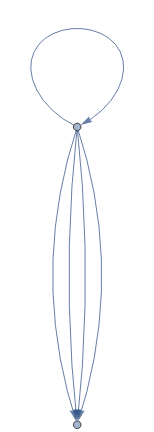
a+b  b+a

x_+y_<->y_+x_
Multiway system of all possible results...
​
Then show a proof path of one of them....
[[ Applying it to an expression, and to a relation ]]
In[]:=
TwoWayMultiReplaceGraphList[{plus[a_,b_]<->plus[b_,a_]},2,"CoSubstitutionLemmas"->True]
Out[]=

,
,

In[]:=
TwoWayMultiReplaceGraphList[{plus[a_,b_]<->plus[b_,a_]},2,"CoSubstitutionLemmas"->False]
Out[]=

,
,

In[]:=
TwoWayMultiReplaceGraphList[{a_⊕b_b_⊕a_,a_⊕(b_⊕c_)(a_⊕b_)⊕c_},2,"CoSubstitutionLemmas"->False]
Out[]=

,
,

In[]:=
VertexList/@%
Out[]=
{{a_⊕b_b_⊕a_,a_⊕(b_⊕c_)(a_⊕b_)⊕c_},{a_⊕b_b_⊕a_,a_⊕b_a_⊕b_,a_⊕(b_⊕c_)(a_⊕b_)⊕c_,a_⊕(b_⊕c_)(a_⊕c_)⊕b_,(a_⊕b_)⊕c_(c_⊕a_)⊕b_,a_⊕(b_⊕c_)(b_⊕a_)⊕c_,a_⊕(b_⊕c_)c_⊕(a_⊕b_),(a_⊕b_)⊕c_(a_⊕b_)⊕c_,a_⊕(b_⊕c_)a_⊕(b_⊕c_)},{a_⊕b_b_⊕a_,a_⊕b_a_⊕b_,a_⊕(b_⊕c_)(a_⊕b_)⊕c_,a_⊕(b_⊕c_)(a_⊕c_)⊕b_,(a_⊕b_)⊕c_(c_⊕a_)⊕b_,a_⊕(b_⊕c_)(b_⊕a_)⊕c_,a_⊕(b_⊕c_)c_⊕(a_⊕b_),(a_⊕b_)⊕c_(a_⊕b_)⊕c_,a_⊕(b_⊕c_)a_⊕(b_⊕c_),a_⊕(b_⊕c_)b_⊕(c_⊕a_),(a_⊕b_)⊕c_a_⊕(c_⊕b_),(a_⊕b_)⊕c_b_⊕(a_⊕c_),a_⊕(b_⊕c_)a_⊕(c_⊕b_),(a_⊕b_)⊕c_c_⊕(a_⊕b_),a_⊕(b_⊕c_)(b_⊕c_)⊕a_,(a_⊕b_)⊕c_a_⊕(b_⊕c_),(a_⊕b_)⊕c_(b_⊕c_)⊕a_,(a_⊕b_)⊕c_(b_⊕a_)⊕c_,(a_⊕b_)⊕c_c_⊕(b_⊕a_),a_⊕(b_⊕c_)(c_⊕b_)⊕a_,(a_⊕b_)⊕c_(c_⊕b_)⊕a_,(a_⊕b_)⊕c_(a_⊕c_)⊕b_,(a_⊕b_)⊕c_b_⊕(c_⊕a_),a_⊕(b_⊕c_)(c_⊕a_)⊕b_,a_⊕(b_⊕c_)b_⊕(a_⊕c_),a_⊕(b_⊕c_)c_⊕(b_⊕a_)}}
In[]:=
Union/@%
Out[]=
{{a_⊕(b_⊕c_)(a_⊕b_)⊕c_,a_⊕b_b_⊕a_},{(a_⊕b_)⊕c_(a_⊕b_)⊕c_,(a_⊕b_)⊕c_(c_⊕a_)⊕b_,a_⊕(b_⊕c_)(a_⊕b_)⊕c_,a_⊕(b_⊕c_)(a_⊕c_)⊕b_,a_⊕(b_⊕c_)(b_⊕a_)⊕c_,a_⊕(b_⊕c_)a_⊕(b_⊕c_),a_⊕(b_⊕c_)c_⊕(a_⊕b_),a_⊕b_a_⊕b_,a_⊕b_b_⊕a_},{(a_⊕b_)⊕c_(a_⊕b_)⊕c_,(a_⊕b_)⊕c_(a_⊕c_)⊕b_,(a_⊕b_)⊕c_(b_⊕a_)⊕c_,(a_⊕b_)⊕c_(b_⊕c_)⊕a_,(a_⊕b_)⊕c_(c_⊕a_)⊕b_,(a_⊕b_)⊕c_(c_⊕b_)⊕a_,(a_⊕b_)⊕c_a_⊕(b_⊕c_),(a_⊕b_)⊕c_a_⊕(c_⊕b_),(a_⊕b_)⊕c_b_⊕(a_⊕c_),(a_⊕b_)⊕c_b_⊕(c_⊕a_),(a_⊕b_)⊕c_c_⊕(a_⊕b_),(a_⊕b_)⊕c_c_⊕(b_⊕a_),a_⊕(b_⊕c_)(a_⊕b_)⊕c_,a_⊕(b_⊕c_)(a_⊕c_)⊕b_,a_⊕(b_⊕c_)(b_⊕a_)⊕c_,a_⊕(b_⊕c_)(b_⊕c_)⊕a_,a_⊕(b_⊕c_)(c_⊕a_)⊕b_,a_⊕(b_⊕c_)(c_⊕b_)⊕a_,a_⊕(b_⊕c_)a_⊕(b_⊕c_),a_⊕(b_⊕c_)a_⊕(c_⊕b_),a_⊕(b_⊕c_)b_⊕(a_⊕c_),a_⊕(b_⊕c_)b_⊕(c_⊕a_),a_⊕(b_⊕c_)c_⊕(a_⊕b_),a_⊕(b_⊕c_)c_⊕(b_⊕a_),a_⊕b_a_⊕b_,a_⊕b_b_⊕a_}}
In[]:=
TwoWayMultiReplaceGraphList[{a_⊕b_b_⊕a_,a_⊕(b_⊕c_)(a_⊕b_)⊕c_},2,"CoSubstitutionLemmas"->False,"Deduplicate"->True]
Out[]=

,
,

In[]:=
VertexList/@%
Out[]=
{{a_⊕b_b_⊕a_,a_⊕(b_⊕c_)(a_⊕b_)⊕c_},{a_⊕b_b_⊕a_,a_⊕b_a_⊕b_,a_⊕(b_⊕c_)(a_⊕b_)⊕c_,a_⊕(b_⊕c_)(a_⊕c_)⊕b_,(a_⊕b_)⊕c_(c_⊕a_)⊕b_,a_⊕(b_⊕c_)(b_⊕a_)⊕c_,a_⊕(b_⊕c_)c_⊕(a_⊕b_),(a_⊕b_)⊕c_(a_⊕b_)⊕c_,a_⊕(b_⊕c_)a_⊕(b_⊕c_)},{a_⊕b_b_⊕a_,a_⊕b_a_⊕b_,a_⊕(b_⊕c_)(a_⊕b_)⊕c_,a_⊕(b_⊕c_)(a_⊕c_)⊕b_,(a_⊕b_)⊕c_(c_⊕a_)⊕b_,a_⊕(b_⊕c_)(b_⊕a_)⊕c_,a_⊕(b_⊕c_)c_⊕(a_⊕b_),(a_⊕b_)⊕c_(a_⊕b_)⊕c_,a_⊕(b_⊕c_)a_⊕(b_⊕c_),(a_⊕b_)⊕c_(b_⊕c_)⊕a_,(a_⊕b_)⊕c_c_⊕(b_⊕a_),a_⊕(b_⊕c_)(c_⊕b_)⊕a_,(a_⊕b_)⊕c_a_⊕(c_⊕b_),(a_⊕b_)⊕c_(c_⊕b_)⊕a_,(a_⊕b_)⊕c_(a_⊕c_)⊕b_,(a_⊕b_)⊕c_b_⊕(c_⊕a_),a_⊕(b_⊕c_)(c_⊕a_)⊕b_,(a_⊕b_)⊕c_c_⊕(a_⊕b_),a_⊕(b_⊕c_)b_⊕(c_⊕a_),(a_⊕b_)⊕c_b_⊕(a_⊕c_),a_⊕(b_⊕c_)b_⊕(a_⊕c_),a_⊕(b_⊕c_)c_⊕(b_⊕a_),a_⊕(b_⊕c_)a_⊕(c_⊕b_),(a_⊕b_)⊕c_(b_⊕a_)⊕c_,a_⊕(b_⊕c_)(b_⊕c_)⊕a_}}
In[]:=
TwoWayMultiReplaceGraphList[{a_⊕b_b_⊕a_,a_⊕(b_⊕c_)(a_⊕b_)⊕c_},3,"CoSubstitutionLemmas"->False,"Deduplicate"->True]
Out[]=

,
,
,

In[]:=
VertexList/@%
Out[]=
{{a_⊕b_b_⊕a_,a_⊕(b_⊕c_)(a_⊕b_)⊕c_},{a_⊕b_b_⊕a_,a_⊕b_a_⊕b_,a_⊕(b_⊕c_)(a_⊕b_)⊕c_,a_⊕(b_⊕c_)(a_⊕c_)⊕b_,(a_⊕b_)⊕c_(c_⊕a_)⊕b_,a_⊕(b_⊕c_)(b_⊕a_)⊕c_,a_⊕(b_⊕c_)c_⊕(a_⊕b_),(a_⊕b_)⊕c_(a_⊕b_)⊕c_,a_⊕(b_⊕c_)a_⊕(b_⊕c_)},{a_⊕b_b_⊕a_,a_⊕b_a_⊕b_,a_⊕(b_⊕c_)(a_⊕b_)⊕c_,a_⊕(b_⊕c_)(a_⊕c_)⊕b_,(a_⊕b_)⊕c_(c_⊕a_)⊕b_,a_⊕(b_⊕c_)(b_⊕a_)⊕c_,a_⊕(b_⊕c_)c_⊕(a_⊕b_),(a_⊕b_)⊕c_(a_⊕b_)⊕c_,a_⊕(b_⊕c_)a_⊕(b_⊕c_),(a_⊕b_)⊕c_(b_⊕c_)⊕a_,(a_⊕b_)⊕c_c_⊕(b_⊕a_),a_⊕(b_⊕c_)(c_⊕b_)⊕a_,(a_⊕b_)⊕c_a_⊕(c_⊕b_),(a_⊕b_)⊕c_(c_⊕b_)⊕a_,(a_⊕b_)⊕c_(a_⊕c_)⊕b_,(a_⊕b_)⊕c_b_⊕(c_⊕a_),a_⊕(b_⊕c_)(c_⊕a_)⊕b_,(a_⊕b_)⊕c_c_⊕(a_⊕b_),a_⊕(b_⊕c_)b_⊕(c_⊕a_),(a_⊕b_)⊕c_b_⊕(a_⊕c_),a_⊕(b_⊕c_)b_⊕(a_⊕c_),a_⊕(b_⊕c_)c_⊕(b_⊕a_),a_⊕(b_⊕c_)a_⊕(c_⊕b_),(a_⊕b_)⊕c_(b_⊕a_)⊕c_,a_⊕(b_⊕c_)(b_⊕c_)⊕a_},{a_⊕b_b_⊕a_,a_⊕b_a_⊕b_,a_⊕(b_⊕c_)(a_⊕b_)⊕c_,a_⊕(b_⊕c_)(a_⊕c_)⊕b_,(a_⊕b_)⊕c_(c_⊕a_)⊕b_,a_⊕(b_⊕c_)(b_⊕a_)⊕c_,a_⊕(b_⊕c_)c_⊕(a_⊕b_),(a_⊕b_)⊕c_(a_⊕b_)⊕c_,a_⊕(b_⊕c_)a_⊕(b_⊕c_),(a_⊕b_)⊕c_(b_⊕c_)⊕a_,(a_⊕b_)⊕c_c_⊕(b_⊕a_),a_⊕(b_⊕c_)(c_⊕b_)⊕a_,(a_⊕b_)⊕c_a_⊕(c_⊕b_),(a_⊕b_)⊕c_(c_⊕b_)⊕a_,(a_⊕b_)⊕c_(a_⊕c_)⊕b_,(a_⊕b_)⊕c_b_⊕(c_⊕a_),a_⊕(b_⊕c_)(c_⊕a_)⊕b_,(a_⊕b_)⊕c_c_⊕(a_⊕b_),a_⊕(b_⊕c_)b_⊕(c_⊕a_),(a_⊕b_)⊕c_b_⊕(a_⊕c_),a_⊕(b_⊕c_)b_⊕(a_⊕c_),a_⊕(b_⊕c_)c_⊕(b_⊕a_),a_⊕(b_⊕c_)a_⊕(c_⊕b_),(a_⊕b_)⊕c_(b_⊕a_)⊕c_,a_⊕(b_⊕c_)(b_⊕c_)⊕a_}}
In[]:=
Length/@%
Out[]=
{2,9,25,25}
In[]:=
TwoWayMultiReplaceGraphList[{x_⊕y_y_⊕x_},3,"CoSubstitutionLemmas"->False,"Deduplicate"->True,"Canonicalize"->False]
Out[]=

,
,
,


Applying the axiom to an expression to make a MW graph

Applying the axiom to a statement

We could add a relation about ↔ itself
Things get tricky because we don’t want the substitution to replace the two-way rule...

Applying the axiom starting just with itself

But using only the axiom every time....

[Cosubstitution]

[Is this a natural mathematical operation, or is it metamathematical?]
Understandable version:
[[ Need to make a token-event graph of this ]]

Accumulative lemmas

Correspondence to FindEquationalProof

Indicate a single path which will have various accumulating lemmas ... and both substitution and co-substitution
(We can make this FEP if the destination node is a ↔ a )

Going beneath binary operators

To be human-level math, it has to be in a cloud....

[ Finding alternative fluid-level math ; what is the homotopy relative to current math ]

Branchial graphs and the historical evolution of math

Fixed axioms vs. accumulative lemmas

Correspondence with FindEquationalProof

Pure substitution vs. other entailments

? parasubstitution

The notion of truth vs stating statements

Going beneath named mathematics

Finding Plus in the wild / identifying Plus in the ruliad

To establish that a particular combinator lump “is” Plus, show the Peano axioms for it ..... though this isn’t quite enough

The theorems of all possible non-standard arithmetics will also show up in the combinator soup