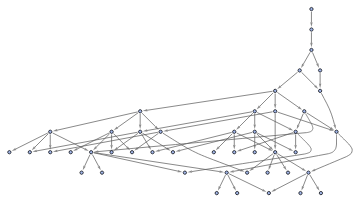
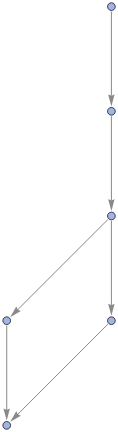
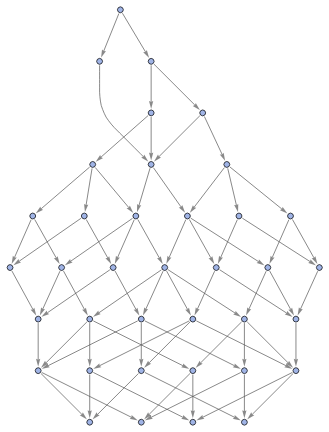
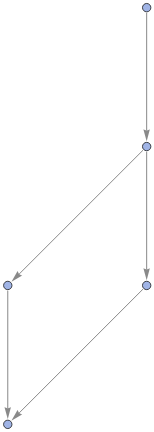
Rules of Inference

First case: (Expression) Substitution

Replace in all possible ways everywhere in the tree
In[]:=
ResourceFunction["MultiReplace"][f[x,g[y]],a_:>h[a]]
Out[]=
{0}{h[f][x,g[y]]},{1}{f[h[x],g[y]]},{2,0}{f[x,h[g][y]]},{2,1}{f[x,g[h[y]]]},{2}{f[x,h[g[y]]]},{}{h[f[x,g[y]]]}
Even at a single position in the expression, multiple rewrites can occur....
In[]:=
ResourceFunction["MultiReplace"][{a,{b,c}},{___,x_,___}:>f[x]]
Out[]=
{2}{{a,f[b]},{a,f[c]}},{}{f[a],f[{b,c}]}
In[]:=
cbrules={s[x_][y_][z_]->x[z][y[z]],k[x_][y_]->x}
Out[]=
{s[x_][y_][z_]x[z][y[z]],k[x_][y_]x}
In[]:=
ResourceFunction["MultiReplace"][k[s][s],cbrules]
Out[]=
{2,{}}{s}
{s[s[s]][s][s][s][s],s[s][s][s[s]][s][s]}
​
In[]:=
ResourceFunction["MultiReplace"][s[s[s]][s][s][s][s],cbrules]
Out[]=
{1,{0,0}}{s[s][s][s[s]][s][s]}
In[]:=
ResourceFunction["MultiReplace"][s[s][s][s[s]][s][s],cbrules]
Out[]=
{1,{0,0}}{s[s[s]][s[s[s]]][s][s]}
In[]:=
ResourceFunction["MultiReplace"][s[s[s][s][s[s][k[k][s]][s]]][s][s][s[k[s][k]][k][s]],cbrules]
Out[]=
{1,{0,0,0,1,1}}{s[s[s][s][s[s][k[k][s][s]]]][s][s][s[k[s][k]][k][s]]},{1,{0,0,0,1}}{s[s[s[s][k[k][s]][s]][s[s[s][k[k][s]][s]]]][s][s][s[k[s][k]][k][s]]},{1,{0}}{s[s][s][s[s][k[k][s]][s]][s][s[s]][s[k[s][k]][k][s]]},{1,{1}}{s[s[s][s][s[s][k[k][s]][s]]][s][s][k[s][k][s][k[s]]]},{2,{0,0,0,1,1,0,1}}{s[s[s][s][s[s][k][s]]][s][s][s[k[s][k]][k][s]]},{2,{1,0,0,1}}{s[s[s][s][s[s][k[k][s]][s]]][s][s][s[s][k][s]]}
In[]:=
Length[%]
Out[]=
6

The ruliology of pure substitution is just like combinators

[ ? look at simpler combinator transformations ]
​

Typed WMs

{f[x_,y_],g[x_,y_,z_],f[x_,z_]}XXXXX

Symbolic System Ruliology

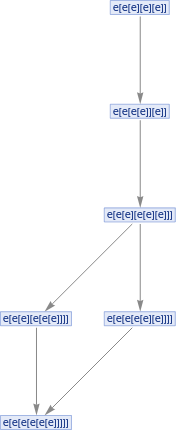
Absolutely minimal “math”

In[]:=
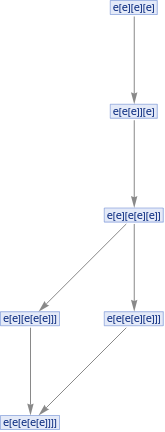
Groupings[Table[e,5],Construct->2]
Out[]=
{e[e][e][e][e],e[e[e][e][e]],e[e[e][e]][e],e[e[e[e][e]]],e[e[e]][e][e],e[e[e[e]][e]],e[e[e[e]]][e],e[e[e[e[e]]]],e[e][e[e]][e],e[e[e][e[e]]],e[e][e][e[e]],e[e][e[e][e]],e[e[e]][e[e]],e[e][e[e[e]]]}
In[]:=
ResourceFunction["MultiwayCombinator"][e[x_][y_]->x[x[y]],#,5,"StatesGraph"]&/@Groupings[Table[e,3],Construct->2]
Out[]=

,

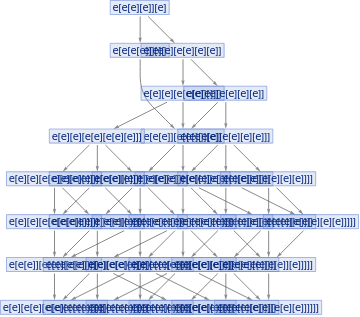
In[]:=
ResourceFunction["MultiwayCombinator"][e[x_][y_]->x[x[y]],#,6,"StatesGraph"]&/@Groupings[Table[e,4],Construct->2]
Out[]=

,
,
,
,

In[]:=
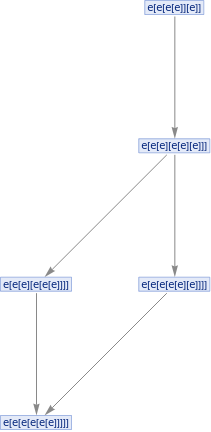
ResourceFunction["MultiwayCombinator"][e[x_][y_]->x[x[y]],#,6,"StatesGraph"]&/@Groupings[Table[e,5],Construct->2]
Out[]=

,
,
,
,
,
,
,
,
,
,
,
,
,

In[]:=
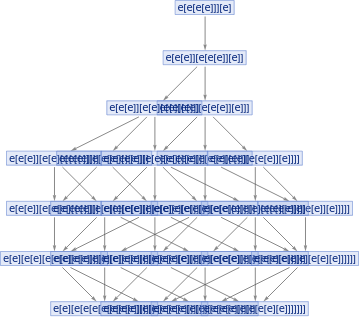
ResourceFunction["MultiwayCombinator"][e[x_][y_]->x[x[y]],#,7,"StatesGraphStructure"]&/@Groupings[Table[e,5],Construct->2]
Out[]=

,
,
,
,
,
,
,
,
,
,
,
,
,

This is all in the “expression interpretation”

Including two-way rule...

This is nontrivial because there are many places in the states to apply the rule....

Rule-based substitution

Applying only the original rule
What about commutativity of ↔ ?

NOTE:
1. This doesn’t use the derived rules; only the original one
2. This is a full-states multiway graph, not a TEG

Applying also the derived rules

Other rules: https://www.wolframscience.com/nks/notes-3-10--other-symbolic-systems-rules/

Proof Correspondence

Substitution Rules on Rules

Given:
we can apply
anywhere in the “a” tree

“Non-learning system” [“Non-rule-building system” | “Non-agglutinative”] : i.e. it doesn’t make new lemmas; it just keeps applying the original axioms

[The version that builds is recursively-building system] [ rules-from-rules system ] [ rulogenic ? ]

With substitution as the only LoI, the vat of e[x_][y_]↔ x_[x_[y_]] doesn’t grow

I.e. this piece of the ruliad is a black hole...

Nodes are theorems

Axioms are

Only the first axiom is taken to be an active thing to be used in substitutions...
In a “faster” system of mathematics (that doesn’t always revert back to its original axioms) this substitution rule could also be applied to “active rules”, to give other active rules

Finding the Simplest Non-Trivial Non-Learning System

These end up with “inner” TwoWayRule’s ......

We are not assuming commutativity of  .....

Add in commutativity of  ...

The disagreement seems to be a foliation issue .... the lhs, rhs sorting didn’t happen quickly enough....
[[ Need to modify the actual multiway combinator code to sort the two-way rule at each step ]]

x <-> x[x]

Does this generate equivalences between all expressions?
I think this generates all equivalences between pairs of expressions
obviously just appends any tree branch to any tree....
I.e. this says that every conceivable theorem is true
I.e.mathematical space is the complete graph ; there is no extension in mathematical space ; everything is connected in one step to everything in the end.....
But ... the building up of mathematics isn’t trivial .... and before you’re “finished” it might seem like you have something nontrivial... And the metamathematical space is nontrivial....
​
Eventually, this grows into the complete graph..... [[ actually ... only its transitive closure will ... ]] This is the one-step-at-a-time proof graph
WHY is x  x missing???

Now consider finding a path in the proof graph to somewhat we assert is true.... [this is more narrow definition of truth]

[[ This is like saying “p is true” rather than just saying “p” ]]
Why is this path not present?

Branchial graphs

These are maps of “peer” theorems .... i.e. ones that lie at particular time after the big bang....
This is an instantaneous state of all possible mathematics, with all possible proofs done.... [this is metamathematical space ... because it is a space generated by all possible proof paths]

Each state in the multiway system is a theorem in mathematics

In this case, we’re not applying derived theorems .... we’re always going back to the “base theorem”
The fact that we’re not applying derived theorems is merely a foliation statement [[[ except that with applying derived theorems we have a 2n multiway graph rather than a 1n multiway graph ]]]

The fact that we’re showing things as two-way rules is just “for amusement value” ... unless we used the derived-rule optimization

Without the 2-way rule fluff, this is equivalent to just saying that every derivable string is a theorem

Truth: either you assert certain axioms are true, and then you deduce everything ... or you assert the axioms but you insist on having some “obviously true” that you show things are equivalent to.

A mathematical observer lives in a certain region of metamathematical branchial space...

The proof cone lets them travel to other parts of metamathematical branchial space [i.e. to other peer theorems]

Motion in metamathematical space is translating to different theorems in the same axiom system

The comparative homogeneity of the space is the statement that it

Motion requires that you can uniformly translate one collection of theorems to another

If the configuration of theorems is dramatically changed as you move in metamathematical space, then you don’t have pure motion....

Basic claim: the mathematical observer only sees a coarse-grained version of metamathematical space

An implication is that they don’t see the non-random-walk proof thread which could be undecidable
Most proof threads terminate somewhere in the equivalence class of the observer
Create a bunch of proof threads (corresponding to the “cross-section” of the observer) ... claim would be that these threads will typically be absorbed by a future observer with a similar cross-section .....
[i.e. they might all mix up in their location within the cross-section of the observer] If you looked at a single thread, you might not see it terminate