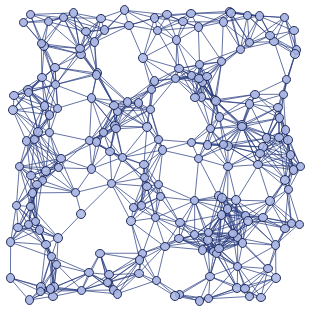
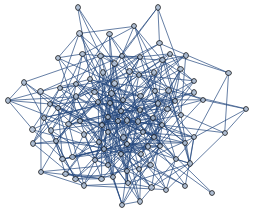
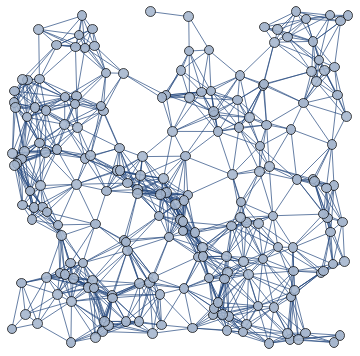
Major effects as edges are removed
Major effects as edges are removed
The effective dimension can increase because removing a fixed fraction of edges has more effect on the interior of a geodesic than the exterior
In[]:=
Range[10]
Out[]=
{1,2,3,4,5,6,7,8,9,10}
In[]:=
GridGraph[{10,10}]
Out[]=
In[]:=
DiscretizeRegion[Rectangle[]]
Out[]=
In[]:=
ResourceFunction["FlatManifoldToGraph"][2,.2,200]["SpatialGraph"]
Out[]=
In[]:=
ResourceFunction["FlatManifoldToGraph"][2,.15,200]["SpatialGraph"]
Out[]=
In[]:=
Graphics[Point[RandomPoint[Rectangle[],200]]]
Out[]=
In[]:=
NearestNeighborGraph[RandomPoint[Rectangle[],200],{All,.15}]
Out[]=
In[]:=
RandomGraph[{100,400}]
Out[]=
In[]:=
Table[NearestNeighborGraph[RandomPoint[Rectangle[],200],{All,f}],{f,.05,.25,.05}]
Out[]=
,
,
,
,
When we estimate dimension or curvature, we are computing V(r) .... we can do this with rmin < r < rmax
Analog of RipleyK for graph distance....
In[]:=
ValuesResourceFunction["WolframHausdorffDimension"]
,All,"AllVolumes","VertexMethod"Identity,"VolumeMethod"Identity
We need it to be above the percolation threshold where there is an infinite cluster with probability 1.
Percolation in graphs
Percolation in graphs
The case of a torus graph
The case of a torus graph
Effective mean field theory
Effective mean field theory
Fraction f of edges have been removed....
Geodesic ball volume r^d
Assume it’s “manifold like” : i.e.
d[f]
d[t]
Dimension measurement
Dimension measurement