Syntax of category theory
Syntax of category theory
Generalization of the syntax
Morphism; functors [ multimorphisms ; operads (n inputs; 1 output) ]
Without transitive closure: have path dependence
Relationship to type theory
Relationship to type theory
Spatialization of limiting versions [?]
Spatialization of limiting versions [?]
Hierarchy
Rulial multiway system
Rulial multiway system
{a->b->c,a->d->c}
In[]:=
Graph[{a->b,b->c,a->d,d->c},VertexLabelsAutomatic]
Out[]=
In[]:=
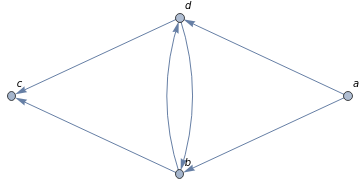
Graph[{a->b,b->c,a->d,d->c,b->d,d->b},VertexLabelsAutomatic]
Out[]=
Necessarily, we’ve defined a face here...
Given a triangle in any graph, it could be a face. [[But ... many cycles in a graph aren’t naturally faces.]]
1 morphism : joins 2 objects [ maps from 0-morphisms to 0-morphisms ]
2 morphism : maps from 1-morphisms to 1-morphisms
2 morphism : maps from 1-morphisms to 1-morphisms
operad : n-ary function mapping from n 0-morphisms to 1 0-morphisms [?]
Space of all symbolic transformation rules
Space of all symbolic transformation rules
Can be decomposed into transformation for things without , and things with
Correspondence with type theory
Correspondence with type theory
A multiway system is like a type; the rules are the type constructor ; the terms of the type are states of the multiway systems ;; paths are proofs of equality
inhabitation of a type: multiway system has at least one state
Set theory
Set theory
{{},{{}},{}}
Only possible base is {}
ur-element : has base elements other than { }
Analog of consciousness constraint for math:
Analog of consciousness constraint for math:
Think only in terms of n-categories for small n....
Light cones: provability cone
Within the coordinate system defined by the slice
Within the coordinate system defined by the slice
“Faster than proof travel”: have to go outside of a given mathematical framework
e.g. Goodstein needs ZFC
e.g. Goodstein needs ZFC