State weighting:
State weighting:
In[]:=
Counts/@MultiwaySystem[{"A""AB","B"->"BA"},"A",6,"AllStatesListUnmerged"]
Out[]=
“Explicit” path weighting
“Explicit” path weighting
In[]:=
MultiwaySystem[{"A""AA","A""A"},"A",4,"EvolutionGraphFull"]
Out[]=
A multiedge is like a trivial critical pair
Tagged path weighting
Tagged path weighting
In[]:=
MultiwaySystem[{"A""AA","A""A"},"A",4,"EvolutionGraphWeighted"]
Out[]=
In[]:=
Graph[MultiwaySystem[{"A""AA","A""A"},"A",4,"EvolutionGraphWeighted"],EdgeLabels"EdgeWeight",EdgeLabelStyleDirective[Red,Large]]
Out[]=
In[]:=
Counts/@MultiwaySystem[{"A""AA","A""A"},"A",6,"AllStatesListUnmerged"]
Out[]=
{A1,AA1,A1,AAA2,AA3,A1,AAAA6,AAA12,AA7,A1,AAAAA24,AAAA60,AAA50,AA15,A1,AAAAAA120,AAAAA360,AAAA390,AAA180,AA31,A1,AAAAAAA720,AAAAAA2520,AAAAA3360,AAAA2100,AAA602,AA63,A1}
In[]:=
Counts/@MultiwaySystem[{"A""AA","AA""A"},"A",6,"AllStatesListUnmerged"]
Out[]=
{A1,AA1,AAA2,A1,AAAA6,AA5,AAAAA24,AAA28,A5,AAAAAA120,AAAA180,AA61,AAAAAAA720,AAAAA1320,AAA662,A61}
In[]:=
Counts/@MultiwaySystem[{"AB""BA","BA""AB"},"ABAB",6,"AllStatesListUnmerged"]
Out[]=
{ABAB1,BAAB1,AABB1,ABBA1,ABAB3,BABA2,BAAB5,AABB3,ABBA5,BBAA2,ABAB13,BABA12,BAAB25,AABB13,ABBA25,BBAA12,ABAB63,BABA62}
In[]:=
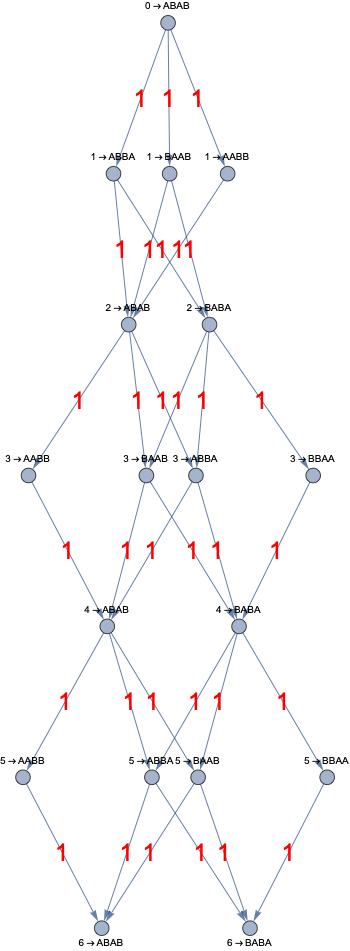
Graph[MultiwaySystem[{"AB""BA","BA""AB"},"ABAB",6,"EvolutionGraphWeighted"],EdgeLabels"EdgeWeight",EdgeLabelStyleDirective[Red,Large],VertexLabelsAutomatic]
Out[]=
In[]:=
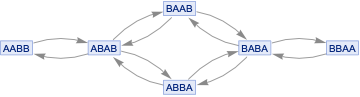
MultiwaySystem[{"AB""BA","BA""AB"},"ABAB",6,"StatesGraph"]
Out[]=
In[]:=
MultiwaySystem[{"AB""BA","BA""AB"},"ABAB",6,"StatesGraph","IncludeEventInstances"True,"IncludeStepNumber"True]
Out[]=
With state IDs (and step numbers) everything is a tree....
At any given step, the token is split equally; then the question is how many states (with different stateIDs) have the same content...
At any given step, the token is split equally; then the question is how many states (with different stateIDs) have the same content...
[ JG algorithm...] [ IncludeStateWeights, IncludeEventWeights ]
[ JG algorithm...] [ IncludeStateWeights, IncludeEventWeights ]
Start with unmerged (StateID, StepNumber)
In everything unmerged, simple flow token based on edges
To make a states graph, just collect up all the items one is considering identical....
Is this equivalent to Bellman-Ford on the states graph???? [not quite]
In everything unmerged, simple flow token based on edges
To make a states graph, just collect up all the items one is considering identical....
Is this equivalent to Bellman-Ford on the states graph???? [not quite]
StatesGraphWeighted
StatesGraphWeighted
A cycle in the states graph [perhaps also a cycle in causal graph]
Condition for states graph to be cycle free?
BranchialGraphWeighted
BranchialGraphWeighted
Concept of weighting
Concept of weighting
You start with a token and every branch it splits equally into evolution edge
In a states graph where there are multiple feeders at different time steps.....