In[]:=
allrules=Import["/Users/sw/Dropbox/Physics/Data/RuleEnumerations/22-42c.wxf"];
In[]:=
Length[allrules]
Out[]=
40405
In[]:=
RandomSample[allrules,20]
Out[]=
In[]:=
TotalCausalInvariantQ[WolframModel[#],1]&/@{{{1,2},{1,3}}{{2,4},{4,2},{3,2},{3,5}},{{1,1},{1,1}}{{2,2},{2,1},{1,3},{4,3}},{{1,2},{1,2}}{{3,2},{3,2},{2,4},{4,5}},{{1,1},{1,2}}{{3,4},{3,1},{4,5},{5,1}},{{1,2},{2,3}}{{1,1},{1,1},{2,2},{4,3}},{{1,2},{3,2}}{{1,3},{3,2},{2,4},{5,2}},{{1,2},{1,2}}{{3,3},{4,3},{4,2},{2,5}},{{1,1},{1,2}}{{3,3},{1,3},{4,1},{5,1}},{{1,2},{2,3}}{{1,4},{1,5},{1,6},{1,7}},{{1,2},{2,3}}{{4,1},{4,5},{1,5},{2,6}},{{1,2},{3,2}}{{1,1},{3,4},{3,2},{4,5}},{{1,1},{1,2}}{{3,2},{3,2},{3,4},{4,5}},{{1,2},{3,2}}{{2,2},{4,1},{4,3},{4,5}},{{1,2},{2,3}}{{4,5},{4,6},{2,5},{3,6}},{{1,2},{2,3}}{{3,4},{4,5},{5,3},{1,2}},{{1,2},{2,3}}{{4,5},{5,3},{2,3},{6,1}},{{1,2},{1,2}}{{3,1},{3,1},{3,4},{1,5}},{{1,2},{2,3}}{{4,4},{4,5},{3,5},{3,2}},{{1,1},{1,2}}{{2,2},{2,1},{2,1},{3,2}},{{1,2},{1,2}}{{2,2},{2,2},{3,2},{1,1}}}
Out[]=
{False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False}
In[]:=
ParallelMapMonitored[TotalCausalInvariantQ[WolframModel[#],1]&,{{{1,2},{1,3}}{{2,4},{4,2},{3,2},{3,5}},{{1,1},{1,1}}{{2,2},{2,1},{1,3},{4,3}},{{1,2},{1,2}}{{3,2},{3,2},{2,4},{4,5}},{{1,1},{1,2}}{{3,4},{3,1},{4,5},{5,1}},{{1,2},{2,3}}{{1,1},{1,1},{2,2},{4,3}},{{1,2},{3,2}}{{1,3},{3,2},{2,4},{5,2}},{{1,2},{1,2}}{{3,3},{4,3},{4,2},{2,5}},{{1,1},{1,2}}{{3,3},{1,3},{4,1},{5,1}},{{1,2},{2,3}}{{1,4},{1,5},{1,6},{1,7}},{{1,2},{2,3}}{{4,1},{4,5},{1,5},{2,6}},{{1,2},{3,2}}{{1,1},{3,4},{3,2},{4,5}},{{1,1},{1,2}}{{3,2},{3,2},{3,4},{4,5}},{{1,2},{3,2}}{{2,2},{4,1},{4,3},{4,5}},{{1,2},{2,3}}{{4,5},{4,6},{2,5},{3,6}},{{1,2},{2,3}}{{3,4},{4,5},{5,3},{1,2}},{{1,2},{2,3}}{{4,5},{5,3},{2,3},{6,1}},{{1,2},{1,2}}{{3,1},{3,1},{3,4},{1,5}},{{1,2},{2,3}}{{4,4},{4,5},{3,5},{3,2}},{{1,1},{1,2}}{{2,2},{2,1},{2,1},{3,2}},{{1,2},{1,2}}{{2,2},{2,2},{3,2},{1,1}}}]
Out[]=
{False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False}
2,2 3,2
2,2 3,2
In[]:=
allrules=Import["/Users/sw/Dropbox/Physics/Data/RuleEnumerations/22-32c.wxf"];
In[]:=
Length[allrules]
Out[]=
4702
ParallelMapMonitored[TotalCausalInvariantQ[WolframModel[#],1]&,allrules];//AbsoluteTiming
In[]:=
Counts[%]
Out[]=
True375,False4327
In[]:=
citest[1]=ParallelMapMonitored[TotalCausalInvariantQ[WolframModel[#],1]&,allrules];
In[]:=
Counts[citest[1]]
Out[]=
True96,False4606
In[]:=
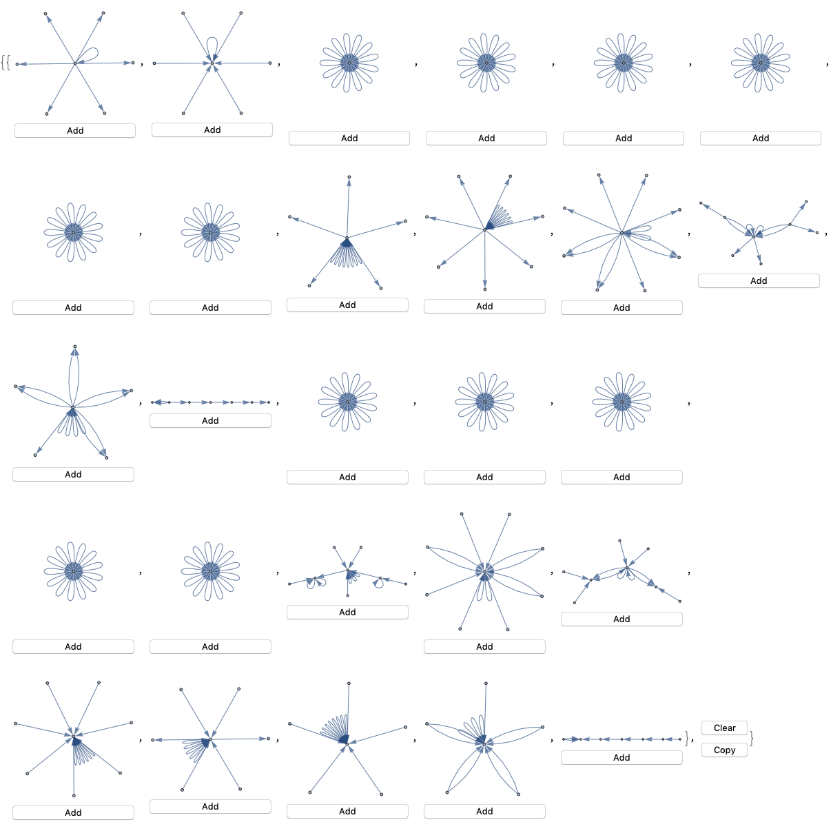
InteractiveListSelectorSW[First/@GatherBy[Select[ParallelMapMonitored[FinalPicture2[#,5]#&,Pick[allrules,citest[1]]],ConnectedGraphQ[UndirectedGraph[First[#]]]&]]]
Out[]=
In[]:=
frules[1]=Pick[allrules,citest[1],False];
In[]:=
frules[t_]:=frules[t]=Pick[frules[t-1],citest[t],False]
In[]:=
citest[t_]:=citest[t]=ParallelMapMonitored[TotalCausalInvariantQ[WolframModel[#],t]&,frules[t-1]];
In[]:=
citest[2]
In[]:=
Counts[citest[2]]
Out[]=
False4485,True121
In[]:=
InteractiveListSelectorSW[First/@GatherBy[Select[ParallelMapMonitored[FinalPicture2[#,5]#&,Pick[frules[1],citest[2]]],ConnectedGraphQ[UndirectedGraph[First[#]]]&]]]
Out[]=
[ More ]
[ More ]