Binary turing machine group structure -- Taliesin Beynon

use permutation group

flipping the head is Cycles[{1,2}]
rotating the tape is {Cycles[{1,3,5,7,...,2n-1}], Cycles[{2,4,6,8,2n}] -- this preserves the state of each cell, but moves them all left (or right, whatever, the inverse takes care of that)

makeBinaryTuringGroup[n_] := ​​ PermutationGroup[Cycles[{{1,2}}], ​​ Cycles[{Range[1,2n-1,2], Range[2,2n,2]}]​​ ];

these are the orders:

In[]:=
Table[GroupOrder@makeBinaryTuringGroup[i],{i,2,10}]
Out[]=
{8,24,64,160,384,896,2048,4608,10240}

plots

In[]:=
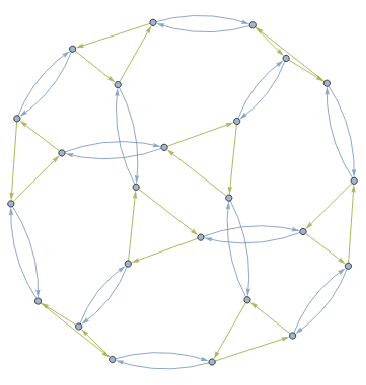
CayleyGraph@makeBinaryTuringGroup[3]
Out[]=
In[]:=
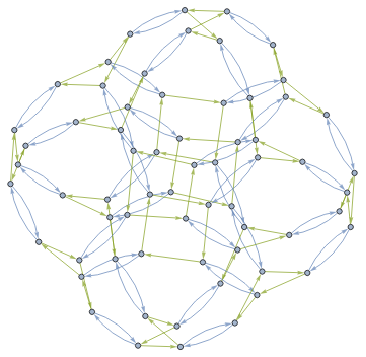
CayleyGraph@makeBinaryTuringGroup[4]
Out[]=

this sequence is https://oeis.org/A036289

this leads to https://mathworld.wolfram.com/Cube-ConnectedCycleGraph.html

The nth order cube-connected cycle can also be constructed as the Cayley graph of the group acting on binary words of length n generated by the group elements that rotate the bits of a word one position left, rotate the bits of a word one position right, and invert the first bit of a word (Akers and Krishnamurthy 1989; Annexstein et al. 1990).

explicit representation as a semidirect product

For an infinite tape we model the TM as a semi-direct product of additive structure of

(representing head position), and

-indexed direct product


2
(representing tape state) whose group multiplication is ⊕ (xor).
The group action is (
z
1
,
t
1
) · (
z
2
,
t
1
) = (
z
1
+
z
2
,
t
1
⊕ (
t
2
>>
z
1
)) , in other words: the offsets of two TM actions just add, but the tape effects are XOR’d together after the second is shifted so that it begins where the first action left the tape head. This is a semidirect product since the one subgroup (z) doesn’t “see” the second subgroup, but that one is affected.
The generators are are just (±1, 0) and (0, 1), where the vector 1 there is the element of


2
whose 0’th element is 1, and all other elements are 0.

​