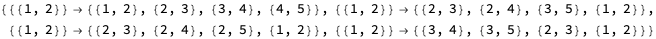“WolframModelRuleProduct”

In[]:=
SetAttributes[WolframModelRuleProduct,Flat]
In[]:=
WolframModelRuleProduct[rule1_Rule,rule2_Rule]:=Module[{unif=First/@HypergraphUnifications[First[rule1],First[rule2]]},FindCanonicalWolframModel[Flatten[Function[i,Map[i#&,Catenate[Last[MultiwaySystem[WolframModel[rule1],#,1,"AllStatesListUnmerged"]]&/@Last[MultiwaySystem[WolframModel[rule2],i,1,"AllStatesListUnmerged"]]]]]/@unif]]]
In[]:=
WolframModelRuleProduct[rule1_,rule2_List]:=Catenate[WolframModelRuleProduct[rule1,#]&/@rule2]
In[]:=
WolframModelRuleProduct[rule1_List,rule2_]:=Catenate[WolframModelRuleProduct[#,rule2]&/@rule1]
In[]:=
WolframModelRuleProduct[{{1,2},{1,3}}{{1,2},{1,4},{2,4},{3,4}},{{1,2},{1,3}}{{1,2},{1,4},{2,4},{3,4}}]
Out[]=
In[]:=
RulePlot[WolframModel[#]]&/@%
Out[]=
In[]:=
WolframModel[%361,Automatic,6,"StatesPlotsList"]
Out[]=
In[]:=
WolframModelRuleProduct[{{x,y}}{{x,y},{y,z}},{{x,y}}{{x,y},{y,z}}]
Out[]=
{{{1,2}}{{1,2},{2,3},{3,4}},{{1,2}}{{2,3},{2,4},{1,2}}}
In[]:=
WolframModelRuleProduct[{{x,y}}{{x,y},{y,z}},{{x,y}}{{x,y},{y,z}},{{x,y}}{{x,y},{y,z}}]
Out[]=
In[]:=
RulePlot[WolframModel[#]]&/@%
Out[]=
In[]:=
MultiwaySystem[WolframModel[%],{{0,0}},2,"StatesGraph",VertexSize1]
Out[]=

Find Group [[[ FIRST VERSION ]]]]

In[]:=
permuteRuleX[lhs_rhs_]:=(Last[#]->((lhs/.Thread[#])rhs))&/@(Function[u,(u#)&/@Permutations[u]]@Union[Flatten[lhs]])
gencases[rule_]:=Map[((First/@#)->FindCanonicalWolframModel[Last/@#])&,Tuples[permuteRuleX/@rule]](*maybewrong*)
selectcases[rule_]:=Cases[gencases[rule],(x_rule)x](*maybewrong*)
In[]:=
FindWolframModelGroup[rule:{__Rule}]:=PermutationGroup[PermutationCycles/@#]&/@selectcases[rule]
In[]:=
selectcasesX[lhs_rhs_]:=Cases[permuteRuleX[lhsrhs],(x_(lhsrhs))x]
In[]:=
FindWolframModelGroup[{}]:={}
In[]:=
FindWolframModelGroup[{{{1,2}}{{1,2},{2,3},{3,4}},{{1,2}}{{2,3},{2,4},{1,2}}}]
Out[]=
{PermutationGroup[{Cycles[{}],Cycles[{}]}]}
In[]:=
FindWolframModelGroup[{{{1,2}}{{1,2},{2,1}}}]
Out[]=
{PermutationGroup[{Cycles[{}]}],PermutationGroup[{Cycles[{{1,2}}]}]}
In[]:=
selectcases[{{{1,2}}{{1,2},{2,1}}}]
Out[]=
{{{1,2}},{{2,1}}}
In[]:=
selectcasesX[{{1,2},{2,3}}{{1,2},{2,3},{3,1}}]
Out[]=
{{1,2,3}}
In[]:=
Clear[selectcasesX]
In[]:=
selectcasesX[{{{1,2},{2,3}}{{1,2},{2,3},{3,1}},{{1,2}}{{1,2},{2,1}}}]
Out[]=
{{{1,2,3}},{{1,2}}}
In[]:=
permuteRuleX[{{1,2},{2,3}}{{1,2},{2,3},{3,1}}]
Out[]=
In[]:=
gencases[{{{1,2},{2,3}}{{1,2},{2,3},{3,1}},{{1,2}}{{1,2},{2,1}}}]
Out[]=
In[]:=
gencases[{{{1,2},{2,3}}{{1,2},{2,3},{3,1}}}]
Out[]=
In[]:=
ParallelMapMonitored[#FindWolframModelGroup[{#}]&,EnumerateWolframModelRules[{{1,2}}{{2,2}}]]
Out[]=

Second Version

Big run

Attempted huge run...