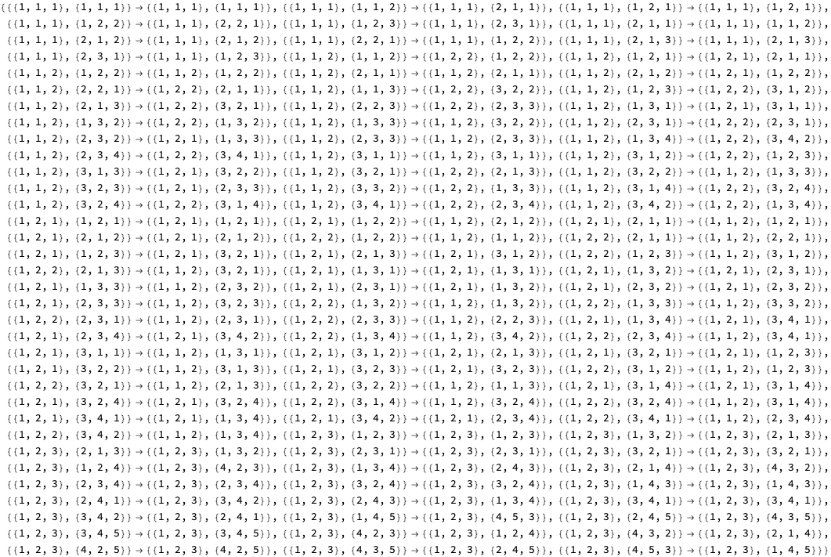In[]:=
EnumerateHypergraphs[{{2,3}}]
Out[]=
In[]:=
ParallelMapMonitored[#->FindCanonicalHypergraph[Map[#[[{3,2,1}]]&,#,{1}]]&,EnumerateHypergraphs[{{2,3}}]]
Out[]=
In[]:=
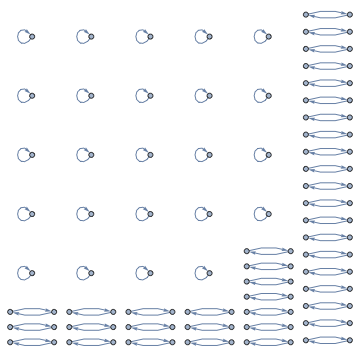
Graph[%]
Out[]=
This is additional isomorphism beyond hypergraph isomorphism, and it’s not very important....
In[]:=
Function[perm,ParallelMapMonitored[#->FindCanonicalHypergraph[Map[#[[perm]]&,#,{1}]]&,EnumerateHypergraphs[{{2,3}}]]]/@Rest[Permutations[Range[3]]]
Out[]=
In[]:=
Graph/@%
Out[]=
In[]:=
Function[perm,Graph[ParallelMapMonitored[#->FindCanonicalHypergraph[Map[#[[perm]]&,#,{1}]]&,EnumerateHypergraphs[{{3,3}}]]]]/@Rest[Permutations[Range[3]]]
Out[]=
Strings
Strings
In[]:=
Graph[#Reverse[#]&/@Tuples[{1,0},4]]
Out[]=
LHS of rule can be permuted....