String Hyperbolicity Test
String Hyperbolicity Test
Edge based
Edge based
In[]:=
<<SetReplace`
In[]:=
lastGenerationModifiedAllEdgesQ[evolution_WolframModelEvolutionObject]:=SameQ@@With[{finalEdges=evolution["StateEdgeIndicesAfterEvent",-1]},evolution["EdgeGenerationsList"]〚finalEdges〛]
In[]:=
lastGenerationModifiedAllEdgesQ[WolframModel[{{1,2}}{{1,3},{1,3},{3,2}},Automatic,4]]
Out[]=
True
In[]:=
lastGenerationModifiedAllEdgesQ[WolframModel[{{1,1,2},{2,3,4}}{{3,3,4},{4,3,2},{1,5,3}},Automatic,Automatic]]
Out[]=
False
In[]:=
WolframModel[{{1,1,2},{2,3,4}}{{3,3,4},{4,3,2},{1,5,3}},Automatic,Automatic,"EdgeCountList"]
Out[]=
{2,3,4,6,8,10,12,14,16,18,20,22,24,26,28,30,32,34,36,38,40,42,44,46,48,50,52,54,56,58,60,62,64,66,68,70,72,74,76,78,80,82,84,86,88,90,92,94,96,98,100,102,104,106,108,110,112,114,116,118,120,122,124,126,128,130,132,134,136,138,140,142,144,146,148,150,152,154,156,158,160,162,164,166,168,170,172,174,176,178,180,182,184,186,188,190,192,194,196,198,200}
In[]:=
lastGenerationModifiedAllEdgesQ[WolframModel[{{1,2},{1,3}}{{2,4},{2,1},{4,1},{4,3}},Automatic,Automatic]]
Out[]=
True
In[]:=
WolframModel[{{1,2},{1,3}}{{2,4},{2,1},{4,1},{4,3}},Automatic,Automatic,"EdgeCountList"]
Out[]=
{2,4,8,16,32,64,128}
In[]:=
lastGenerationModifiedAllEdgesQ[WolframModel[{{1,2}}{{1,3},{3,2}},{{1,2}},3]]
Out[]=
True
In[]:=
lastGenerationModifiedAllEdgesQ[WolframModel[{{1,2}}{{1,3},{3,2},{1,2,3}},{{1,2}},3]]
Out[]=
False
In[]:=
lastGenerationModifiedAllEdgesQ[WolframModel[{{1,2},{2,3}}{{1,2},{2,3},{3,4}},{{1,2},{2,3}},3]]
Out[]=
False
In[]:=
lastGenerationModifiedAllEdgesQ[WolframModel[{{1,2},{2,3}}{{1,2},{2,3},{3,4},{4,5}},{{1,2},{2,3}},3]]
Out[]=
True
Vertex based (less natural in my opinion, but weaker condition)
Vertex based (less natural in my opinion, but weaker condition)
In[]:=
lastGenerationModifiedAllVerticesQ[evolution_WolframModelEvolutionObject]:=With[{finalVertices=Union@Catenate@evolution["FinalState"],generationsList=evolution["EdgeGenerationsList"]},With[{eachVertexEdges=First/@Position[evolution["AllExpressions"],e_List/;!FreeQ[e,#],{1}]&/@finalVertices},With[{vertexMaxGenerations=Max/@(generationsList〚#〛&/@eachVertexEdges)},SameQ@@vertexMaxGenerations]]]
In[]:=
lastGenerationModifiedAllVerticesQ[WolframModel[{{1,2}}{{1,3},{1,3},{3,2}},Automatic,4]]
Out[]=
True
In[]:=
lastGenerationModifiedAllVerticesQ[WolframModel[{{1,1,2},{2,3,4}}{{3,3,4},{4,3,2},{1,5,3}},Automatic,Automatic]]
Out[]=
False
In[]:=
WolframModel[{{1,1,2},{2,3,4}}{{3,3,4},{4,3,2},{1,5,3}},Automatic,Automatic,"VertexCountList"]
Out[]=
{1,2,3,5,7,9,11,13,15,17,19,21,23,25,27,29,31,33,35,37,39,41,43,45,47,49,51,53,55,57,59,61,63,65,67,69,71,73,75,77,79,81,83,85,87,89,91,93,95,97,99,101,103,105,107,109,111,113,115,117,119,121,123,125,127,129,131,133,135,137,139,141,143,145,147,149,151,153,155,157,159,161,163,165,167,169,171,173,175,177,179,181,183,185,187,189,191,193,195,197,199}
In[]:=
lastGenerationModifiedAllVerticesQ[WolframModel[{{1,2},{1,3}}{{2,4},{2,1},{4,1},{4,3}},Automatic,Automatic]]
Out[]=
True
In[]:=
WolframModel[{{1,2},{1,3}}{{2,4},{2,1},{4,1},{4,3}},Automatic,Automatic,"EdgeCountList"]
Out[]=
{2,4,8,16,32,64,128}
In[]:=
WolframModel[{{1,2},{2,3}}{{1,2},{2,3},{3,1}},{{1,2},{2,3}},3,"StatesPlotsList"]
Out[]=
In[]:=
lastGenerationModifiedAllEdgesQ[WolframModel[{{1,2},{2,3}}{{1,2},{2,3},{3,1}},{{1,2},{2,3}},#]]&/@Range[10]
Out[]=
{True,False,True,True,False,False,False,True,True,False}
In[]:=
lastGenerationModifiedAllVerticesQ[WolframModel[{{1,2},{2,3}}{{1,2},{2,3},{3,1}},{{1,2},{2,3}},#]]&/@Range[10]
Out[]=
{True,True,True,True,True,True,True,True,True,True}
In[]:=
WolframModel[{{1,2},{2,3}}{{1,2},{2,3},{3,4}},{{1,2},{2,3}},5,"StatesPlotsList"]
Out[]=
In[]:=
lastGenerationModifiedAllVerticesQ[WolframModel[{{1,2},{2,3}}{{1,2},{2,3},{3,4}},{{1,2},{2,3}},#]]&/@Range[10]
Out[]=
{True,False,False,False,False,False,False,False,False,False}
In[]:=
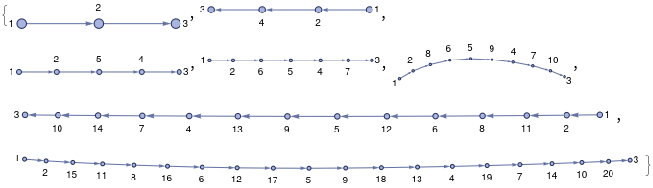
WolframModel[{{1,2},{2,3}}{{1,2},{2,4},{4,3}},{{1,2},{2,3}},6]["StatesPlotsList",VertexLabelsAutomatic]
Out[]=
In[]:=
lastGenerationModifiedAllVerticesQ[WolframModel[{{1,2},{2,3}}{{1,2},{2,4},{4,3}},{{1,2},{2,3}},#]]&/@Range[10]
Out[]=
{True,False,True,True,False,True,False,True,True,False}
In[]:=
lastGenerationModifiedAllEdgesQ[WolframModel[{{1,2},{2,3}}{{1,2},{2,4},{4,3}},{{1,2},{2,3}},#]]&/@Range[10]
Out[]=
{True,False,True,True,False,False,False,True,True,False}
Comments
Comments
In any case, I don’t think this is the right way to do it because we will likely need many layers for a continuum limit to make sense.