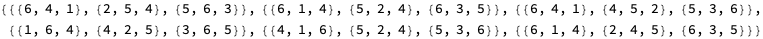RulePlot[WolframModel[{{1,2,3,4}}{{1,4,6},{2,5,4},{3,6,5}}]]
Out[]=
HypergraphPlot@WolframModel[{{1,2,3}}{{6,1,4},{2,4,5},{6,3,5}},{{1,2,3}},3,"FinalState"]
Out[]=
In[]:=
Table[RandomSample/@{{6,1,4},{2,4,5},{6,3,5}},6]
Out[]=
In[]:=
DeleteDuplicates[Table[RandomSample/@{{6,1,4},{2,4,5},{6,3,5}},6]]
Out[]=
In[]:=
HypergraphPlot@WolframModel[{{1,2,3}}#,{{1,2,3}},3,"FinalState"]&/@%
Out[]=
In[]:=
HypergraphPlot@WolframModel[{{1,2,3}}#,{{1,2,3}},3,"FinalState"]&/@%
Out[]=
In[]:=
DeleteDuplicates[{{{6,4,1},{2,5,4},{5,6,3}},{{6,1,4},{5,2,4},{6,3,5}},{{6,4,1},{4,5,2},{5,3,6}},{{1,6,4},{4,2,5},{3,6,5}},{{4,1,6},{5,2,4},{5,3,6}},{{6,1,4},{2,4,5},{6,3,5}}}]
Out[]=
{{6,1,4},{2,4,5},{6,3,5}}
In[]:=
GridGraph[{2,2,2}]
Out[]=
In[]:=
EdgeList[%]
Out[]=
{12,13,15,24,26,34,37,48,56,57,68,78}
In[]:=
List@@@%
Out[]=
{{1,2},{1,3},{1,5},{2,4},{2,6},{3,4},{3,7},{4,8},{5,6},{5,7},{6,8},{7,8}}
In[]:=
Rest/@TableVertexOutComponent
,i,1,{i,8}
Out[]=
{{2,3,5},{1,4,6},{1,4,7},{2,3,8},{1,6,7},{2,5,8},{3,5,8},{4,6,7}}
In[]:=
HypergraphPlot/@WolframModel[{{1,2,3}}->{{2,3,5},{1,4,6},{1,4,7},{2,3,8},{1,6,7},{2,5,8},{3,5,8},{4,6,7}},{{1,2,3}},3,"StatesList"]
Out[]=
In[]:=
GraphData["TetrahedralGraph"]
Out[]=
In[]:=
EdgeList[%]
Out[]=
{12,13,14,23,24,34}
In[]:=
List@@@%
Out[]=
{{1,2},{1,3},{1,4},{2,3},{2,4},{3,4}}
In[]:=
Rest/@TableVertexOutComponent
,i,1,{i,4}
Out[]=
{{2,3,4},{1,3,4},{1,2,4},{1,2,3}}
In[]:=
GraphPlot[SimpleGraph[HypergraphToGraph[#]]]&/@WolframModel[{{1,2,3}}{{1,4,6},{2,5,4},{3,6,5}},{{2,3,4},{1,3,4},{1,2,4},{1,2,3}},4,"StatesList"]
4-ary edges
4-ary edges