In[]:=
Tetrahedron[]
Out[]=
Tetrahedron[]
In[]:=
Graphics3D[TruncatedPolyhedron[Tetrahedron[],1/3]]
Out[]=
In[]:=
Graphics3D/@NestList[TruncatedPolyhedron[#,1/2]&,Tetrahedron[],4]
Out[]=
In[]:=
Graphics3D/@NestList[TruncatedPolyhedron[#,1/3]&,Tetrahedron[],4]
Out[]=
In[]:=
GraphAutomorphismGroup[TorusGraph[{5,5}]]
Out[]=
In[]:=
GraphAutomorphismGroup
Out[]=
CayleyGraph
In[]:=
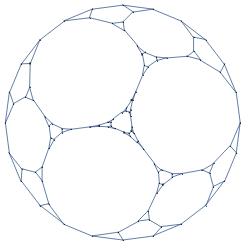
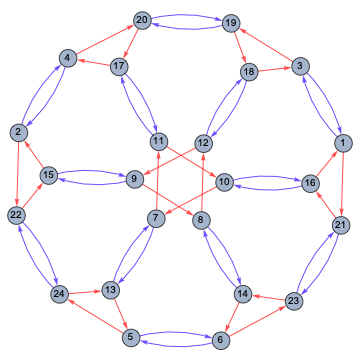
CayleyGraph[PermutationGroup[{Cycles[{{1,5,4}}],Cycles[{{3,4}}]}],VertexLabelsPlaced["Name",Center],VertexSize0.4]
Out[]=
In[]:=
GraphAutomorphismGroup[%]
Out[]=
In[]:=
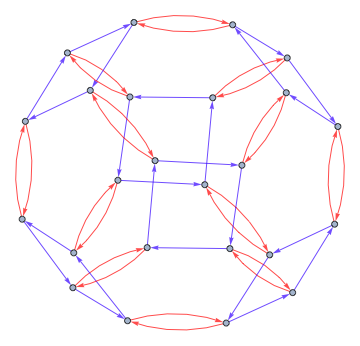
CayleyGraph[SymmetricGroup[4]]
Out[]=
In[]:=
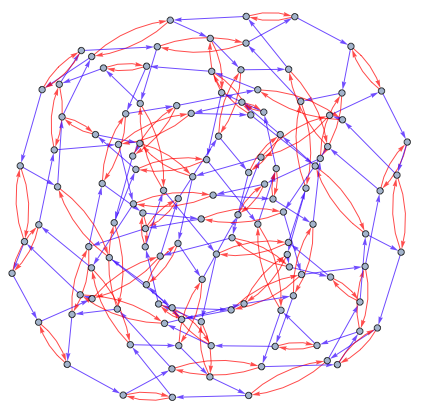
CayleyGraph[SymmetricGroup[5]]
Out[]=
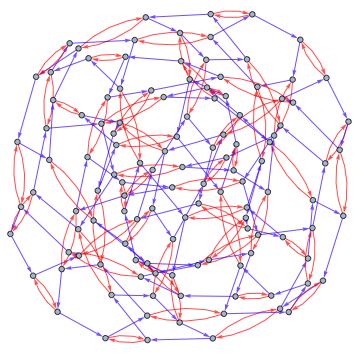
In[]:=
CayleyGraph[SymmetricGroup[5]]
Out[]=
Direct product of cyclic groups:
In particular, Gromov’s theorem and the Bass–Guivarch formula imply that the order of polynomial growth of a finitely generated group is always either an integer or infinity (excluding for example, fractional powers).