In[]:=
allrules=Import["/Users/sw/Dropbox/Physics/Data/RuleEnumerations/22-22c.wxf"];
In[]:=
Length[allrules]
Out[]=
562
In[]:=
t10=Flatten/@List@@@EdgeList@TorusGraph[{10}]
Out[]=
{{1,2},{2,3},{3,4},{4,5},{5,6},{6,7},{7,8},{8,9},{9,10},{10,1}}
In[]:=
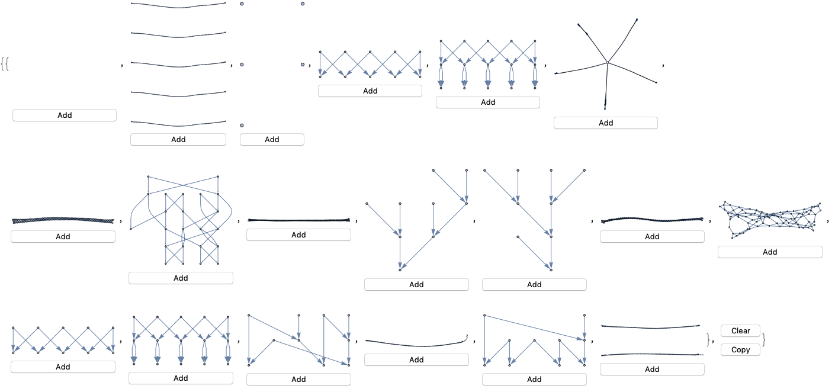
InteractiveListSelectorSW[First/@GatherBy[ParallelMapMonitored[Graph[Rule@@@(WolframModelTest[#,t10]["FinalState"])]#&,allrules],First]]
Out[]=
In[]:=
InteractiveListSelectorSW[First/@GatherBy[ParallelMapMonitored[Graph[Rule@@@(WolframModelTest[#,t10]["EvolutionObject"]["CausalGraph"])]#&,allrules],First]]
Out[]=
In[]:=
ParallelMapMonitored[With[{w=WolframModel[#,t10,20]},{HypergraphPlot[w["FinalState"]],w["CausalGraph"]}]&,{{{1,2},{2,3}}{{1,3},{1,3}},{{1,2},{2,3}}{{1,1},{2,3}},{{1,2},{2,3}}{{2,2},{1,3}},{{1,2},{2,3}}{{3,1},{3,2}},{{1,2},{2,3}}{{1,3},{1,4}},{{1,2},{2,3}}{{3,3},{1,2}}}]
Out[]=
In[]:=
ParallelMapMonitored[With[{w=WolframModel[#,t10,30]},{HypergraphPlot[w["FinalState"]],w["CausalGraph"]}]&,{{{1,2},{2,3}}{{1,3},{1,3}},{{1,2},{2,3}}{{1,1},{2,3}},{{1,2},{2,3}}{{2,2},{1,3}},{{1,2},{2,3}}{{3,1},{3,2}},{{1,2},{2,3}}{{1,3},{1,4}},{{1,2},{2,3}}{{3,3},{1,2}}}]
Out[]=
“Particles”
“Particles”
Arity 3
Arity 3