In[]:=
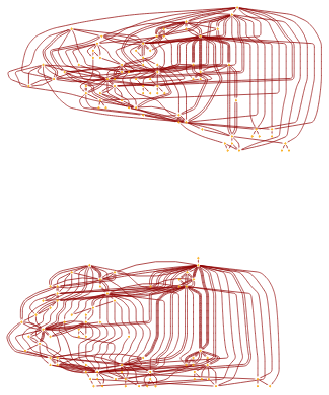
MultiwayTuringMachine[{2506,3506},{1,{{},0}},10,"CausalGraphStructure"]
Out[]=
In[]:=
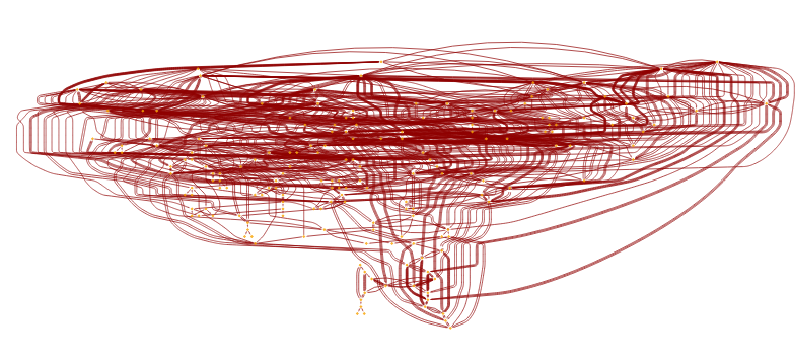
LayeredGraphPlot[MultiwayTuringMachine[{2506,3506},{1,{{},0}},10,"CausalGraphStructure"]]
Out[]=
In[]:=
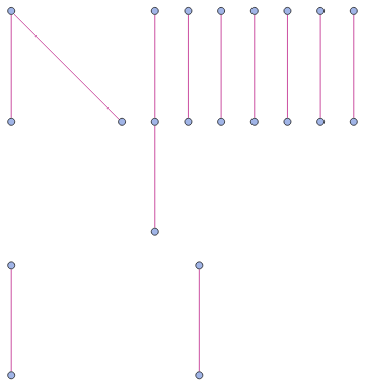
LayeredGraphPlot[MultiwayTuringMachine[{2506,3506},{1,{{},0}},10,"BranchialGraphStructure"]]
Out[]=
In[]:=
RandomInteger[{0,4095},2]
Out[]=
{3604,2189}
In[]:=
LayeredGraphPlot[MultiwayTuringMachine[{3604,2189},{1,{{},0}},10,"CausalGraphStructure"]]
Out[]=
In[]:=
LayeredGraphPlot[MultiwayTuringMachine[{3604,2189},{1,{{},0}},10,"BranchialGraphStructure"]]
Out[]=
In[]:=
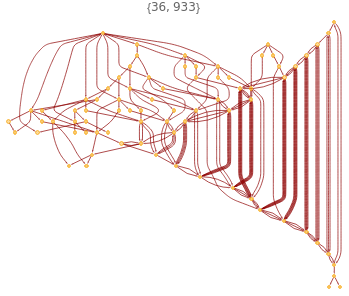
ResourceFunction["ParallelMapMonitored"][LayeredGraphPlot[MultiwayTuringMachine[#,{1,{{},0}},10,"CausalGraphStructure"],PlotLabel#]&,RandomInteger[{0,4095},{10,2}]]
SubKernels`SubKernels
::timekernels
:Timeout for subkernels. Received only 0 of 12 connections.
​
Out[]=
In[]:=
ResourceFunction["ParallelMapMonitored"][LayeredGraphPlot[MultiwayTuringMachine[#,{1,{{},0}},10,"StatesGraphStructure"],PlotLabel#]&,RandomInteger[{0,4095},{10,2}]]
Need 3 TMs to get nontrivial branchial behavior.....

Find pairs of TMs that are causal invariant....

Displaying multispace for TMs??

[[ Do graph layout for multiway system, then use this to lay out the TM in space ]]

One-Case Changes

This was a mixed rule, by mistake:

Note: need to index into existing list....
Transients: