Code
Code
Results
Results
For Boolean algebra, there are immediately truth values defined:
In[]:=
MultiwayOperatorSystem[{And[a_,b_]And[b,a],Or[a_,b_]Or[b,a],And[a_,Or[b_,Not[b_]]]a,Or[a_,And[b_,Not[b_]]]a,a_Module[{b=Unique[]},And[a,Or[b,Not[b]]]],a_Module[{b=Unique[]},Or[a,And[b,Not[b]]]],And[a_,Or[b_,c_]]Or[And[a,b],And[a,c]],Or[And[a_,b_],And[a_,c_]]And[a,Or[b,c]],Or[a_,And[b_,c_]]And[Or[a,b],Or[a,c]],And[Or[a_,b_],Or[a_,c_]]Or[a,And[b,c]]},{And[a,b]},1,"StatesGraph"]
Out[]=
In[]:=
MultiwayOperatorSystem[{And[a_,b_]And[b,a],Or[a_,b_]Or[b,a],And[a_,Or[b_,Not[b_]]]a,Or[a_,And[b_,Not[b_]]]a,a_Module[{b=Unique[]},And[a,Or[b,Not[b]]]],a_Module[{b=Unique[]},Or[a,And[b,Not[b]]]],And[a_,Or[b_,c_]]Or[And[a,b],And[a,c]],Or[And[a_,b_],And[a_,c_]]And[a,Or[b,c]],Or[a_,And[b_,c_]]And[Or[a,b],Or[a,c]],And[Or[a_,b_],Or[a_,c_]]Or[a,And[b,c]]},{And[a,b]},3,"StatesGraphStructure"]
Out[]=
Operator-implemented pattern strings
Operator-implemented pattern strings
"A#B""#AB#"
In[]:=
MultiwayOperatorSystem[{CircleDot[a_,CircleDot[b_,c_]]CircleDot[CircleDot[a,b],c],CircleDot[CircleDot[a_,b_],c_]CircleDot[a,CircleDot[b,c]],CircleDot[a,CircleDot[x_,b]]CircleDot[x,CircleDot[a,CircleDot[b,x]]]},{CircleDot[a,CircleDot[CircleDot[x,y],b]]},3,"StatesGraph"]
Out[]=
In[]:=
MultiwayOperatorSystem[{Equal[a_,b_]Equal[b,a],CircleDot[a_,CircleDot[b_,c_]]CircleDot[CircleDot[a,b],c],CircleDot[CircleDot[a_,b_],c_]CircleDot[a,CircleDot[b,c]],aCircleDot[a,b]},{CircleDot[a,a]CircleDot[a,CircleDot[CircleDot[a,b],b]]},1,"StatesGraph"]
Out[]=
In[]:=
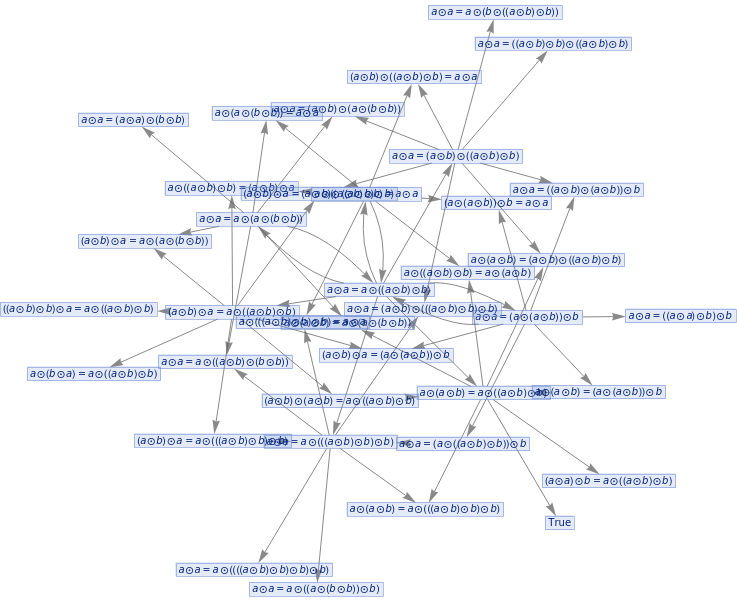
mwo=MultiwayOperatorSystem[{Equal[a_,b_]Equal[b,a],CircleDot[a_,CircleDot[b_,c_]]CircleDot[CircleDot[a,b],c],CircleDot[CircleDot[a_,b_],c_]CircleDot[a,CircleDot[b,c]],aCircleDot[a,b]},{CircleDot[a,a]CircleDot[a,CircleDot[CircleDot[a,b],b]]},2,"StatesGraph"]
Out[]=
(Internally, everything is a string, so there is no evaluation)
Interpretation
Interpretation
Axioms
Lemmas
Theorems
Rule of inference
Axioms
Lemmas
Theorems
Rule of inference
Lemmas
Theorems
Rule of inference
In traditional math, distinguish axioms from rules of inference
In traditional math, distinguish axioms from rules of inference
Fundamental rule is: ab, a gives b
Case 1 (NKS): axioms are the same as rules of inference
Case 1 (NKS): axioms are the same as rules of inference
I.e. axioms are S S multiway rules
Math starts from “True”, and deduces other true statements
Each state is then a proposition of mathematics
Theorem: a state that is derived from True
Lemma: also derived from True, but is S1 S2
Combination rules for applying axioms/lemmas inside other states [things have subparts that are like themselves] [substitute wherever you feel like]
(“Substitution” in first-order logic)
Case 1a: generative mathematics [start from True; prove everything]
Case 1a: generative mathematics [start from True; prove everything]
Case 1b: proofial mathematics: start from a proposition, and reduce it to True [ this isn’t obviously possible, unless the arrows go both ways ]
Case 1b: proofial mathematics: start from a proposition, and reduce it to True [ this isn’t obviously possible, unless the arrows go both ways ]
Or rather, get to something we already know is true (e.g. to prove BA axioms, go from the statement of axioms to a known axiom system statement)
A typical practical theorem is hypothesis assertion (i.e. conclusion) ; something considered free-floating (e.g. an axiom) is True conclusion
Process of going down the multiway system is “entailment” ( https://en.wikipedia.org/wiki/Logical_consequence )
[[[ To get False results, negate after the fact ;;; probably cannot “prove from False” ]]]
Case 2 (traditional) : rules of inference are separate from axioms
Case 2 (traditional) : rules of inference are separate from axioms
Axioms are initial conditions
Law of inference: basically the time evolution operator
Sequent operator:
FindEquationalProof
FindEquationalProof
Case 1: equational
Case 1: equational
Case 2: unidirectional
Case 2: unidirectional
(Mostly need axioms for And and Not etc.)
Claim is that each expression contains e.g. both a and ab
Group theory multiway system
Group theory multiway system
“Algebraic theory” ~~ equality is the top-level predicate
“Algebraic theory” ~~ equality is the top-level predicate
Fields are the cross-over from algebra to analysis
Algebraic theories: always 2-way multiway systems
Algebraic theories: always 2-way multiway systems
The “Model Tradeoff”
The “Model Tradeoff”
Crush every slice of the foliation to a single representative of an equivalence class; then whether something follows is a “straight shot”
Crush every slice of the foliation to a single representative of an equivalence class; then whether something follows is a “straight shot”
That you can change the foliation and get the same answer is causal invariance
Is A ⊢ B and A ⊢ C
Extensionality : means (bidirectional entailment) is equivalent to equivalence
Extensionality : means (bidirectional entailment) is equivalent to equivalence
x = y implies x ⊢ y and y ⊢ x
Univalence: homotopy equivalence is equivalent to equivalence : is directly causal invariance
A ⊢ B and A ⊢ C
Univalence IMPLIES causal invariance .... but not the other way around
Univalence is the justification for completions.
Univalence is normally used in the context of type systems.
If there is a common ancestor, then the states can be considered as equivalent
If two statements can be both be derived from a common hypothesis, then they are equivalent
[ “coarse-grainability” ] [ contractability ]
[ meta-metamathematical principle ]
[ “proof path invariance” ]
[ “ancestry is what counts” ]
[ decendency ]
[ sibling equivalence ] [ ancestral equivalence ] [ sibling indistinguishability ]
derivability implies equivalence
“If things can be derived from a common thing, then those things can be considered equivalent”
derivation identity
equivalability ;;; branchial contractibility ;;; branch contractability ;; branch condensation ;; branch conflation
branch equivalence
< Univalence: there is only one kind of equivalence >
[ meta-metamathematical principle ]
[ “proof path invariance” ]
[ “ancestry is what counts” ]
[ decendency ]
[ sibling equivalence ] [ ancestral equivalence ] [ sibling indistinguishability ]
derivability implies equivalence
“If things can be derived from a common thing, then those things can be considered equivalent”
derivation identity
equivalability ;;; branchial contractibility ;;; branch contractability ;; branch condensation ;; branch conflation
branch equivalence
< Univalence: there is only one kind of equivalence >
Branch equivalence
Branch equivalence
Physical space: contractability of light cones in coarse-graining
Branchial space: completability of branch pairs for measurement
Rulial space: equivalence through PCE
Metamathematical space (AKA proof space): fundamental assumption made in math
(if a single hypothesis implies two different statements, the truth values of the statements must be equivalent)
[ we don’t need such a long list of theorems, because many are equivalent ]
(Zorn’s lemma = axiom of choice = well-ordering = ..... [ many theorems are equivalent ] )
Branchial space: completability of branch pairs for measurement
Rulial space: equivalence through PCE
Metamathematical space (AKA proof space): fundamental assumption made in math
(if a single hypothesis implies two different statements, the truth values of the statements must be equivalent)
[ we don’t need such a long list of theorems, because many are equivalent ]
(Zorn’s lemma = axiom of choice = well-ordering = ..... [ many theorems are equivalent ] )
When you do coarse-graining, you’re not changing the topology .... and therefore you can still make certain coarse-grained statements (without getting into the microweeds)
You can make progress in math by keeping a limited number of theorems; or: it isn’t going to give you much more speedup to have 5 parallel freeways
You can make progress in math by keeping a limited number of theorems; or: it isn’t going to give you much more speedup to have 5 parallel freeways
“branch equivalence” is a meta-axiomatic principle: a principle about generating MW rules [AKA entailment rules]
“branch equivalence” is a meta-axiomatic principle: a principle about generating MW rules [AKA entailment rules]
By completing, you’ve reduced all proof paths to one path....
But which path depends on which foliation you picked.
But which path depends on which foliation you picked.
Physics: By using branch equivalence, you can “complete out” the irreducible details
CS: Branch equivalence is basically the statement that NDTMs (and QTMs) do the same as DTMs
You can coarse grain out the non-determinism
You can coarse grain out the non-determinism
Math: “One proof is enough” Ordinary substitution lemmas allow timelike jump-ahead;
critical pair lemmas [which rely on branch equivalence] all branchlike choices are condensed
critical pair lemmas [which rely on branch equivalence] all branchlike choices are condensed
Analogies
Analogies
Energy is associated with lemmas that we will reuse
(expressing things in terms of lemmas [AKA higher-order definitions] is like abstraction)
(expressing things in terms of lemmas [AKA higher-order definitions] is like abstraction)
< We can measure “abstraction towers” from towers of definitions in theorem banks >
Lemmas are a choice. I.e. you can arrange energy in metamathematical space
If you have a LOT of lemmas, some of them have to be critical pair lemmas, which will eventually force convergence [ like forming black holes ]
Lemmas are a choice. I.e. you can arrange energy in metamathematical space
If you have a LOT of lemmas, some of them have to be critical pair lemmas, which will eventually force convergence [ like forming black holes ]