In[]:=
FindEquationalProof[g[a],{ForAll[x,Implies[f[x],g[x]]],f[a]}]
Out[]=
ProofObject
In[]:=
FindEquationalProof[f[a],{ForAll[x,Implies[f[x],g[x]]],g[a]}]
Out[]=
$Aborted
In[]:=
FindEquationalProof[f[a]g[a],{ForAll[x,f[x]g[x]]}]
Out[]=
ProofObject
In[]:=
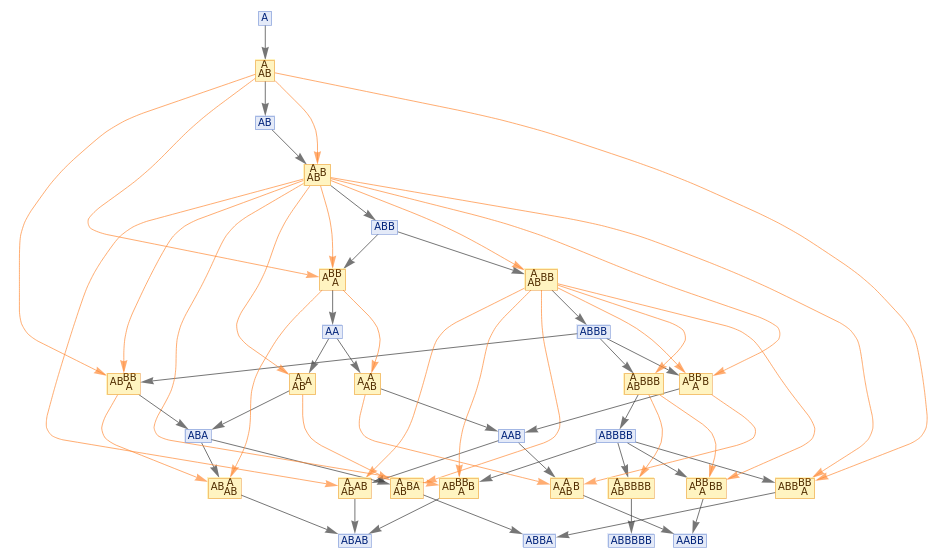
ResourceFunction["MultiwaySystem"][{"A""AB","BB""A"},{"A"},5,"StatesGraph"]
Out[]=
Need to add implicational axiom systems
Need to add implicational axiom systems
In[]:=
ResourceFunction["MultiwaySystem"][{"A""A=B","BB""A"},{"A"},5,"StatesGraph"]
Out[]=
Rules: AB ABB
[ Every edge is using a node ]
In[]:=
FindEquationalProof[i[a],{ForAll[x,Implies[f[x],g[x]]],ForAll[x,Implies[g[x],h[x]]],ForAll[x,Implies[h[x],i[x]]],f[a]}]
Out[]=
ProofObject
Causality is the result of thinking about how substrings work
In[]:=
ResourceFunction["MultiwaySystem"][{"A""AB","BB""A"},{"A"},5,"EvolutionCausalGraph"]
Out[]=
These are subinferences....
Applying a proposition to a string is to say True -> proposition
Applying a proposition to a string is to say True -> proposition
Or there can be hypotheses that are only conditionally true, which correspond to pairs here....
Models
Models
Imposing a model is a way to not have trouble with branching of paths [foliation: folds all points at a given level to the same point]
Causal invariance means imposing a model does not ultimately gain anything <AKA GR is true>
Group multiway system
Group multiway system