Basic idea: make the expressions in the hypergraph have “built-in meanings”, corresponding to statements/predicates
Basic idea: make the expressions in the hypergraph have “built-in meanings”, corresponding to statements/predicates
{Equal,x,y}
{Equal,"AB","BA"}
{ConsistsOf,"AB","A","B"}
{ConsistsOf,"AB",{"A","B"}}
can be represented as
{{ConsistsOf,"AB",x},{IsAList,x,"A","B"}}
In a triplestore, it’s just entity, property, value [i.e. a ternary hyperedge]
In our case, we include arrays, that are higher-k hyperedges.
We encode “knowledge” as hyperedges
We encode “knowledge” as hyperedges
In[]:=
ResourceFunction["MultiwaySystem"][{"AB""BA","BA""AB"},"BBAA",6,"StatesGraph"]
Out[]=
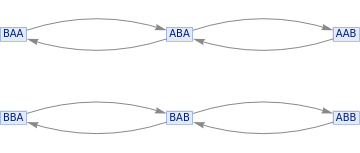
I.e. AABB = BBAA
In the “content” formulation, this becomes a hyperedge
In the “content” formulation, this becomes a hyperedge
{EqualityContents,x,"AABB","BBAA"}
The evolution rule takes multiple hyperedges and “does inference” on them...
Claim: every hyperedge represents an equality
Claim: every hyperedge represents an equality
{"AABB","BBAA"}
The rule for the system is simply the application of that equality in another equality
{{x,y},{u,v}}{{SubstitutionSystem[uv][x],y},{x,y},{u,v}}
Really the internal edges are unordered (to represent equalities)
{{x,y},{u,v}}
In[]:=
ResourceFunction["MultiwaySystem"][{"AB""BA","BA""AB"},ResourceFunction["StringTuples"]["AB",3],6,"StatesGraph"]
Out[]=
In[]:=
ResourceFunction["MultiwaySystem"][{"AB""BA","BA""AB"},ResourceFunction["StringTuples"]["AB",4],6,"StatesGraph"]
Out[]=
In[]:=
TransitiveClosureGraph[%]
Out[]=
Axiom:
In[]:=
ResourceFunction["MultiwaySystem"][{"AB""BA","BA""AB"},ResourceFunction["StringTuples"]["AB",2],6,"StatesGraph"]
Out[]=
Add an axiom that says
{{x,y},{u,v}}{{StringJoin[x,u],StringJoin[y,v]},{x,y},{u,v}}
Rules of inference:
Rules of inference:
{{x,y},{u,v}}{{StringJoin[x,u],StringJoin[y,v]},{x,y},{u,v}}
{{x,y},{u,v}}{{SubstitutionSystem[uv][x],y},{x,y},{u,v}}
[[ may also need the replacement done on the second element ]]
In general, the second rule could be generating multiple outputs.....
{{x,y}}:>{{StringJoin[x,x],StringJoin[y,y]},{x,y}}
Implementation
Implementation
{{x,y},{u,v}}{{StringJoin[x,u],StringJoin[y,v]},{x,y},{u,v}}
In[]:=
SubsetReplace[{{"A","B"},{"BA","AB"}},{{{x_,y_},{u_,v_}}Splice[{{StringJoin[x,u],StringJoin[y,v]},{x,y},{u,v}}],{{x_,y_}}Splice[{{StringJoin[x,x],StringJoin[y,y]},{x,y}}]}]
Out[]=
{{ABA,BAB},{A,B},{BA,AB}}
In[]:=
SubsetReplace[{{"A","B"},{"BA","AB"}},Reverse@{{{x_,y_},{u_,v_}}Splice[{{StringJoin[x,u],StringJoin[y,v]},{x,y},{u,v}}],{{x_,y_}}Splice[{{StringJoin[x,x],StringJoin[y,y]},{x,y}}]}]
Out[]=
{{AA,BB},{A,B},{BABA,ABAB},{BA,AB}}
“Free theorems”
“Free theorems”
In[]:=
NestList[SubsetReplace[#,Reverse@{{{x_,y_},{u_,v_}}Splice[{{StringJoin[x,u],StringJoin[y,v]},{x,y},{u,v}}],{{x_,y_}}Splice[{{StringJoin[x,x],StringJoin[y,y]},{x,y}}]}]&,{{"A","A"}},3]
Out[]=
{{{A,A}},{{AA,AA},{A,A}},{{AAAA,AAAA},{AA,AA},{AA,AA},{A,A}},{{AAAAAAAA,AAAAAAAA},{AAAA,AAAA},{AAAA,AAAA},{AA,AA},{AAAA,AAAA},{AA,AA},{AA,AA},{A,A}}}
In[]:=
NestList[SubsetReplace[#,Reverse@{{{x_,y_},{u_,v_}}Splice[{{StringJoin[x,u],StringJoin[y,v]},{x,y},{u,v}}],{{x_,y_}}Splice[{{StringJoin[x,x],StringJoin[y,y]},{x,y}}]}]&,{{"A","B"}},3]
Out[]=
{{{A,B}},{{AA,BB},{A,B}},{{AAAA,BBBB},{AA,BB},{AA,BB},{A,B}},{{AAAAAAAA,BBBBBBBB},{AAAA,BBBB},{AAAA,BBBB},{AA,BB},{AAAA,BBBB},{AA,BB},{AA,BB},{A,B}}}
In[]:=
NestList[SubsetReplace[#,Reverse@{{{x_,y_},{u_,v_}}Splice[{{StringJoin[x,u],StringJoin[y,v]},{x,y},{u,v}}],{{x_,y_}}Splice[{{StringJoin[x,x],StringJoin[y,y]},{x,y}}]}]&,{{"A","B"},{"A","A"},{"B","B"}},3]
Out[]=
{{{A,B},{A,A},{B,B}},{{AA,BB},{A,B},{AA,AA},{A,A},{BB,BB},{B,B}},{{AAAA,BBBB},{AA,BB},{AA,BB},{A,B},{AAAA,AAAA},{AA,AA},{AA,AA},{A,A},{BBBB,BBBB},{BB,BB},{BB,BB},{B,B}},{{AAAAAAAA,BBBBBBBB},{AAAA,BBBB},{AAAA,BBBB},{AA,BB},{AAAA,BBBB},{AA,BB},{AA,BB},{A,B},{AAAAAAAA,AAAAAAAA},{AAAA,AAAA},{AAAA,AAAA},{AA,AA},{AAAA,AAAA},{AA,AA},{AA,AA},{A,A},{BBBBBBBB,BBBBBBBB},{BBBB,BBBB},{BBBB,BBBB},{BB,BB},{BBBB,BBBB},{BB,BB},{BB,BB},{B,B}}}
[ This is only running the first rule ]
Adding substitution rule
Adding substitution rule
In[]:=
NestList[SubsetReplace[#,Reverse@{{{x_,y_},{u_,v_}}Splice[{{StringJoin[x,u],StringJoin[y,v]},{x,y},{u,v}}],{{x_,y_}}Splice[{{StringJoin[x,x],StringJoin[y,y]},{x,y}}],{{x_,y_},{u_,v_}}Splice[{{Echo@StringReplace[x,Echo[uv]],y},{x,y},{u,v}}]}]&,{{"A","B"},{"A","A"},{"B","B"}},3]
Random rule application
Random rule application
Multiway version?
Multiway version?
This is the spatial graph at this stage....
[[ We
Give it an obviously true fact, and it will generate other true facts......
Equivalence
Equivalence
Case 1: consider equalities (including axioms) to be represented by edges; then simply “apply all edges” using rules of inference in all possible ways
Case 1: consider equalities (including axioms) to be represented by edges; then simply “apply all edges” using rules of inference in all possible ways
Initial condition consists of axioms and “obviously true” equalities [which can also be viewed as axioms]
The obviously true equalities contain “starting” LHS or RHSes of theorem
The obviously true equalities contain “starting” LHS or RHSes of theorem
[ This is trivially causal invariant ]
Case 2: consider equalities to be represented by paths; axioms are “one-step paths”
[Is the transitive closure of #2 is the same as #1?]
Case 2: consider equalities to be represented by paths; axioms are “one-step paths”
[Is the transitive closure of #2 is the same as #1?]
[Is the transitive closure of #2 is the same as #1?]
Initial condition consists of all possible “starting” LHS or RHS
Rules of inference
Rules of inference
[ Evaluation order is somewhat arbitrary, because of StringReplace ]
[[ We can also have a one-way version, not with equality, but e.g. with ordering ]]
Direct multiway system
Direct multiway system
Non-Fixed Length Example
Non-Fixed Length Example
[[[ Depends on the evaluation order which lemmas are applied at each step; this case is doing “generational” updates ]]]
Question: do we put lemmas “in the bag”?
Question: do we put lemmas “in the bag”?
Fuller Version [and CORRECT]
Fuller Version [and CORRECT]
Case 1: Every edge represents an equality [equational logic]
Case 1: Every edge represents an equality [equational logic]
The “state of the universe” is a collection of theorems, with each theorem corresponding to an edge.
Case 2: Equalities are represented by paths
Case 2: Equalities are represented by paths
[[[ Where are the self loops ? ]]]
Case 2a: Every edge is an equality
Case 2a: Every edge is an equality
[[[ This is not an “ended system”; depends on evolution order ]]]
Beyond Duality
Beyond Duality
The reason for the duality above is that in case 1, “space” is just made of edges, just like a multiway graph is made of edges.
With different rules of inference, “space” could work differently.
With different rules of inference, “space” could work differently.
Modus Ponens Inference
Modus Ponens Inference
Only one input for each event.
modus ponens : A , A B / B
Two-way inference is equivalence
Equational Proof Graph
Equational Proof Graph
Adding a critical pair lemma: {“ABAA”,”AAAB”}