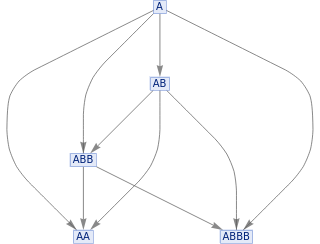
In[]:=
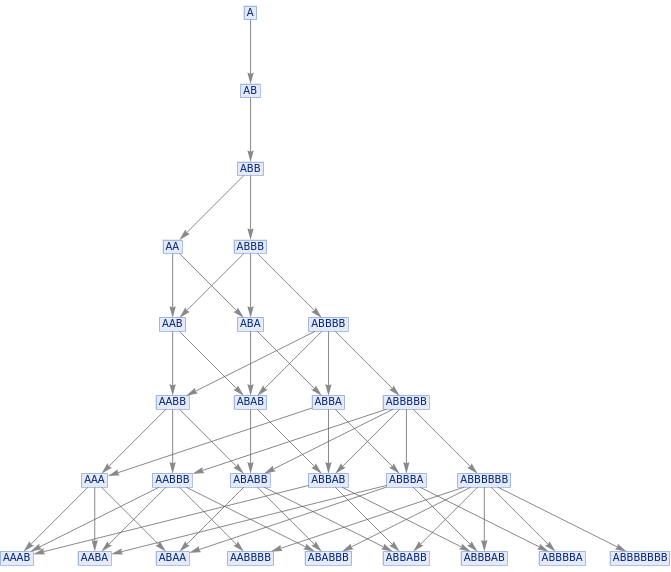
ResourceFunction["MultiwaySystem"][{"A""AB","BB""A"},{"A"},7,"StatesGraph"]
Out[]=
In[]:=
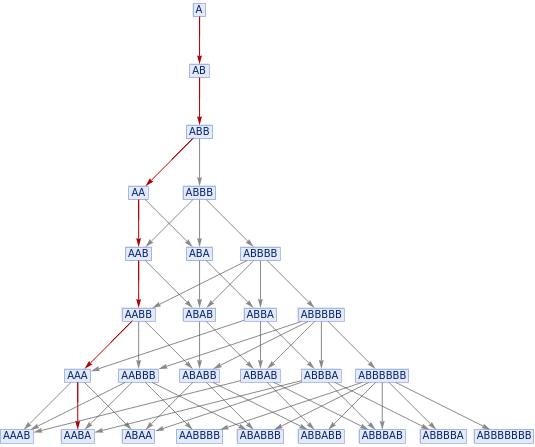
With[{g=ResourceFunction["MultiwaySystem"][{"A""AB","BB""A"},{"A"},7,"StatesGraph"]},HighlightGraph[g,Subgraph[g,PathGraph[FindShortestPath[g,"A","AABA"]]]]]
Out[]=
In[]:=
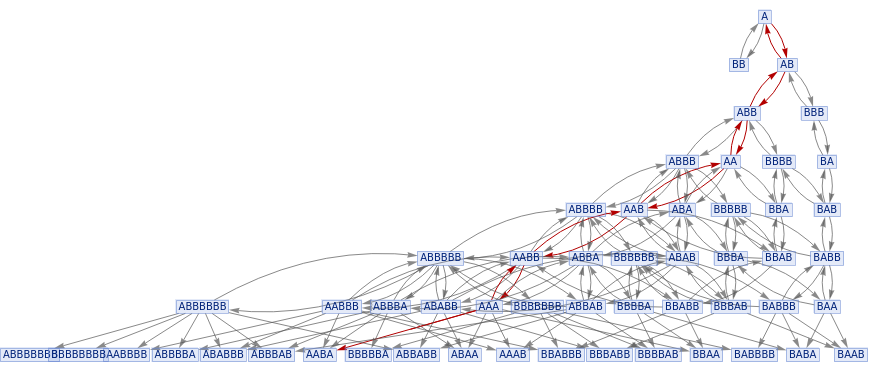
With[{g=ResourceFunction["MultiwaySystem"][{"A""AB","BB""A","AB""A","A""BB"},{"A"},7,"StatesGraph"]},HighlightGraph[g,Subgraph[g,PathGraph[FindShortestPath[g,"A","AABA"],DirectedEdgesTrue]]]]//LayeredGraphPlot
Out[]=
In[]:=
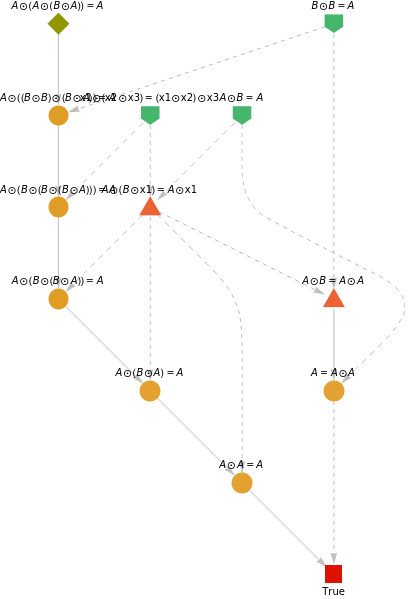
With[{g=ResourceFunction["FindStringProof"][{"A""AABA"},{"A""AB","BB""A"}]["ProofGraph"]},Graph[g,VertexLabels(#[[1]]#[[2,1,2,1,2]]&/@Options[g,"AnnotationRules"][[1,2]])]]
Out[]=
Every substitution X = Y has an evolution edge and a causal edge
After transitive closure, the causal edges in the proof graph are the same as in the MW graph
In[]:=
TransitiveClosureGraph[ResourceFunction["MultiwaySystem"][{"A""AB","BB""A"},{"A"},3,"StatesGraph"]]
Out[]=
In[]:=
ResourceFunction["MultiwaySystem"][{"A""AB","BB""A","A""AAB"},{"A"},4,"StatesGraph"]//LayeredGraphPlot
Out[]=
[ semantic entailment ]
[ rules of inference ]
proposition: a = b
Case 1: every node is a proposition; a true theorem is a path from a proposition node to the True node
Case 2: every node is a word, and theorems are paths between “equivalent” words
Generational states ↔ theorems “in the bag”
Generational states ↔ theorems “in the bag”
A jump ahead event is causally connected to all its component events. [Though in the proof graph, only one causal edge is shown here] [ Because the proof graph is essentially a transitive reduction ]
Looking at centrality of lemmas:
Multiway to Equational
Multiway to Equational
Can have unidirectional string case ... but involves lots of infrastructure
Can have unidirectional string case ... but involves lots of infrastructure
Causal edges: making use of previous expr, and also previous jump-ahead theorem
Causal edges: making use of previous expr, and also previous jump-ahead theorem
Inevitably “positive mass”, because previous results just increase number of different paths.
Critical fact: you put the whole proof in the bag, and use it as a one-step theorem [univalence]
Critical fact: you put the whole proof in the bag, and use it as a one-step theorem [univalence]
Assumption : metamath is explored on geodesics ; therefore you don’t get to see all the theorems of this axiom system
Assumption : metamath is explored on geodesics ; therefore you don’t get to see all the theorems of this axiom system
Dynamical theory of epistemology
To be “about something” is to make everything deterministic; i.e. a total order
To be “about something” is to make everything deterministic; i.e. a total order
Transportability of category theory : uniformity of metamathematical space
Transportability of category theory : uniformity of metamathematical space
Expansion of MM universe: all the computer experiments you could do
Expansion of MM universe: all the computer experiments you could do
Expansion of rulial space : NKS is necessary; math can’t reach far enough [ NKS : quantum computer ; math : classical computer ]
Expansion of rulial space : NKS is necessary; math can’t reach far enough [ NKS : quantum computer ; math : classical computer ]