Idealizations of mathematics
Idealizations of mathematics
Equational logic
Equational logic
exprs + two-way rules
Theorem network
Theorem network
lemma
Multiway systems
Multiway systems
exprs + one-way rules
Inference systems
Inference systems
modus ponens : A , A B / B
{x,xy}y
propositions + parametrized propositions (AKA axiom schemas)
For strings, we are asserting S
Our axioms are all just string assertions X
Our axioms are all just string assertions X
Module[{a},With[{t=a⊼(a⊼a),i=#1⊼(#2⊼#2)&},Join[Thread[axiomst],{i[t⊼(b⊼c),c]t,i[t,b]b,i[i[a,b],b]i[i[b,a],a]}]]]
In[]:=
Module[{a},With[{t=a⊼(a⊼a),i=#1⊼(#2⊼#2)&},Join[Thread[{(a⊼(b⊼c))⊼(((d⊼c)⊼((a⊼d)⊼(a⊼d)))⊼(a⊼(a⊼b)))}t],{i[t⊼(b⊼c),c]t,i[t,b]b,i[i[a,b],b]i[i[b,a],a]}]]]
Out[]=
{((a$355592⊼(b⊼c))⊼(((d⊼c)⊼((a$355592⊼d)⊼(a$355592⊼d)))⊼(a$355592⊼(a$355592⊼b))))(a$355592⊼(a$355592⊼a$355592)),(((a$355592⊼(a$355592⊼a$355592))⊼(b⊼c))⊼(c⊼c))(a$355592⊼(a$355592⊼a$355592)),((a$355592⊼(a$355592⊼a$355592))⊼(b⊼b))b,((a$355592⊼(b⊼b))⊼(b⊼b))((b⊼(a$355592⊼a$355592))⊼(a$355592⊼a$355592))}
In[]:=
BooleanMinimize[a⊼(a⊼a)]
Out[]=
True
Examples
Examples
In[]:=
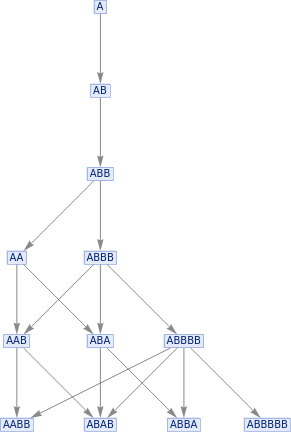
ResourceFunction["MultiwaySystem"][{"A""AB","BB""A"},{"A"},5,"StatesGraph"]
Out[]=
In[]:=
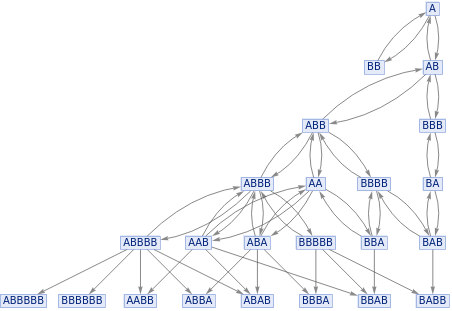
ResourceFunction["MultiwaySystem"][Join[#,Reverse/@#]&@{"A""AB","BB""A"},{"A"},5,"StatesGraph"]//LayeredGraphPlot
Out[]=
Is a one-way multiway system an idealization of modus ponens?
“Modus Ponens” Multiway System
“Modus Ponens” Multiway System
"ABBAAAAA"
{{"AB","BAA"},{"BAA","AAA"}}
Say we have proved so far:
{"AB"->"BAA","BAA"->"AAA"}
Let’s imagine our axioms are:
{"A""AB","BB""A"}
What can we derive?
Can we apply these to substrings?
ResourceFunction["MultiwaySystem"][{"A""AB","BB""A"},{"A"},5,"StatesGraph"]
First step: we have a bag of transformation rules
{"A""AB","BB""A"}
Apply the transformation rules to a starting string....
This generates a bunch of derived transformation rules. Now we take each generated state, and apply not just the original rules, but also the derived transformation rules.
Encoding logic
Encoding logic
nand expr nand expr
In[]:=
BooleanTable[Nand[Nand[a,b],Nand[a,b]],{a,b}]
Out[]=
{True,False,False,False}
In[]:=
BooleanTable[a,{a,b}]
Out[]=
{True,True,False,False}
For equational logic, want to know for which operator tables, blah = blah
https://www.wolframscience.com/nks/p781--implications-for-mathematics-and-its-foundations/ : things equivalent to true
Can we do sub-substitution with implication:
(a.b).(b.c)(a.c)
((x.y).(y.z)).(w.x)
((x.y).(y.z)).(w.x)(x.z).(w.x)(*???*)
In[]:=
Nand[False,True]
Out[]=
True
In[]:=
FalseTrue
Out[]=
True
In[]:=
Nand[True,True]
Out[]=
False
Claim: does work for Equal; doesn’t work for Implies
Conversion from modus ponens to equational
Conversion from modus ponens to equational
Assuming :
(1)ppqq(2)q(pp)q(3)(pq)q(qp)p
Then
{ap.p,a.bp.p}
yields
b=p.p
In[]:=
Implies[p,p]//BooleanMinimize
Out[]=
True
{b==(p.p).b}(*byaxiom2*)
{ba.b}(*byfirstassertion*)
Picture of idealized math
Picture of idealized math
expressions are propositions
arrows are “follows from” (which might be implication) [ nothing but substitutions ]
arrows are “follows from” (which might be implication) [ nothing but substitutions ]
“Ancient Greek ‘implication’” : “material implication”
Perhaps “intuitionistic implication”
In the derivation of a theorem, I might use several previous theorems, or I might just use axioms.
Theorem is a pair here. Proof is the path from one part of the pair to the other.
Given a multiplication table, I can color equal items in this picture....
I can find a multiplication table that agrees with the axioms
(Completeness : model can give everything the axioms give)