Decidability of a theory implies a bound on the lengths of proofs
Decidability of a theory implies a bound on the lengths of proofs
[ How long is the bound? Does it depend on the expressions? ]
Expr Expr vs. Theorem(s) Theorem
Expr Expr vs. Theorem(s) Theorem
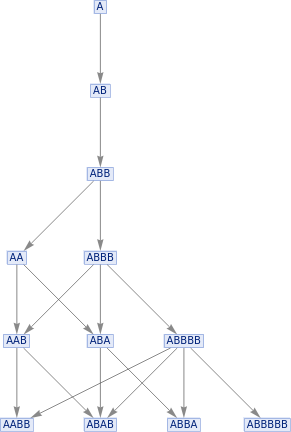
In[]:=
ResourceFunction["MultiwaySystem"][{"A""AB","BB""A"},{"A"},5,"StatesGraph"]
Out[]=
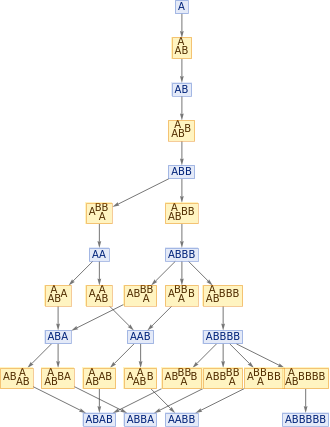
In[]:=
ResourceFunction["MultiwaySystem"][{"A""AB","BB""A"},{"A"},5,"EvolutionEventsGraph"]
Out[]=
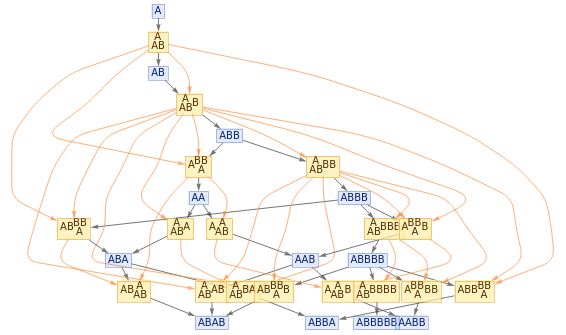
In[]:=
ResourceFunction["MultiwaySystem"][{"A""AB","BB""A"},{"A"},5,"EvolutionCausalGraph"]
Out[]=
Pick out “Interesting” Theorems
Pick out “Interesting” Theorems
Which cannot be deduced from ones earlier in the list? For Exprs, ask what the order of sizes are
In[]:=
ResourceFunction["MultiwaySystem"][{"A""AB","BB""A"},{"A"},7]
Out[]=
{{A},{AB},{ABB},{AA,ABBB},{AAB,ABA,ABBBB},{AABB,ABAB,ABBA,ABBBBB},{AAA,AABBB,ABABB,ABBAB,ABBBA,ABBBBBB},{AAAB,AABA,AABBBB,ABAA,ABABBB,ABBABB,ABBBAB,ABBBBA,ABBBBBBB}}
Rulial multiway graph
Rulial multiway graph
In[]:=
ResourceFunction["MultiwaySystem"][Flatten[ResourceFunction["EnumerateSubstitutionSystemRules"][{22},2]],ResourceFunction["StringTuples"]["AB",4],4,"StatesGraph"]//LayeredGraphPlot
Out[]=
This is only inequivalent rules.....
In[]:=
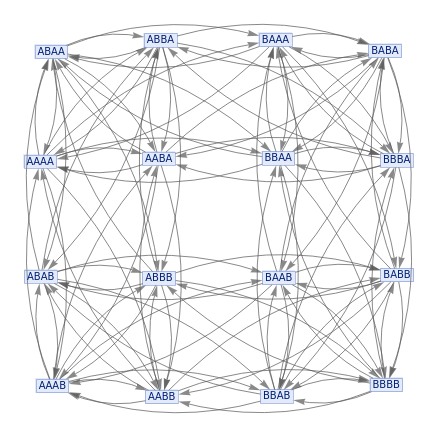
ResourceFunction["MultiwaySystem"][Flatten[ResourceFunction["EnumerateSubstitutionSystemRules"][{22},2]],ResourceFunction["StringTuples"]["AB",2],4,"StatesGraph"]//LayeredGraphPlot
Out[]=
In[]:=
ResourceFunction["EnumerateSubstitutionSystemRules"][{22},2]
Out[]=
{{AAAA},{AAAB},{AABB},{ABAA},{ABAB},{ABBA}}
All possible rules
All possible rules
In[]:=
Outer[Rule,ResourceFunction["StringTuples"]["AB",2],ResourceFunction["StringTuples"]["AB",2]]//Flatten
Out[]=
{AAAA,AAAB,AABA,AABB,ABAA,ABAB,ABBA,ABBB,BAAA,BAAB,BABA,BABB,BBAA,BBAB,BBBA,BBBB}
In[]:=
ResourceFunction["MultiwaySystem"][Outer[Rule,ResourceFunction["StringTuples"]["AB",2],ResourceFunction["StringTuples"]["AB",2]]//Flatten,ResourceFunction["StringTuples"]["AB",4],8,"StatesGraph"]
Out[]=
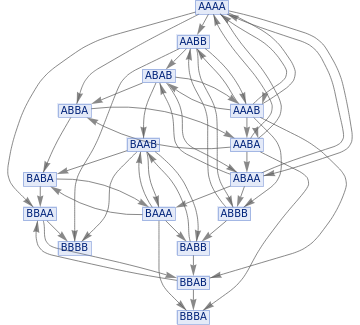
Single Multiway System
Single Multiway System
[ Can be thought of either as a fibration, or as a foliation ]
[ Can be thought of either as a fibration, or as a foliation ]
Theorem Lengths
Theorem Lengths
Euclid
Euclid