In[]:=
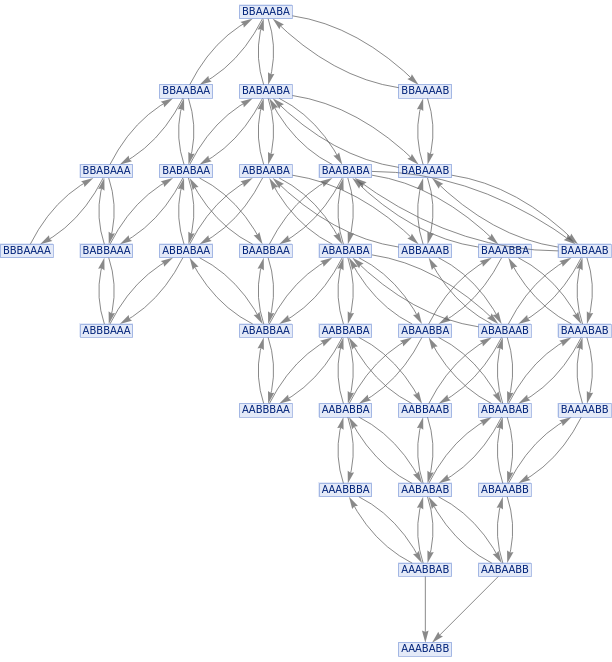
ResourceFunction["MultiwaySystem"][{"AB""BA","BA""AB"},"BBAAABA",8,"StatesGraph",GraphLayout"LayeredDigraphEmbedding"]
Out[]=
In[]:=
FindShortestPath[ResourceFunction["MultiwaySystem"][{"AB""BA","BA""AB"},"BBAAABA",8,"StatesGraph",GraphLayout"LayeredDigraphEmbedding"],"BBAAABA","AAABABB"]
Out[]=
{BBAAABA,BABAABA,ABBAABA,ABABABA,AABBABA,AABABBA,AAABBBA,AAABBAB,AAABABB}
In[]:=
MultiwayGroup[<|"Generators"generators_List,"Relations"relations_List,"Identity"identity_,"Inverses"inverses_List|>,stepCount_Integer,rest___]:=Module[{stringGenerators,stringRelations,stringIdentity,stringInverses,generatorRules,relationRules,identityRules,inverseRules},stringGenerators=ToString/@generators;stringRelations=(ToString[First[#]]ToString[Last[#]])&/@relations;stringIdentity=ToString[identity];stringInverses=ToString/@inverses;generatorRules=DeleteDuplicates[Catenate[Module[{generator=#},generatorStringJoin[generator,#]&/@Join[stringGenerators,{stringIdentity},stringInverses]]&/@Join[stringGenerators,{stringIdentity},stringInverses]]];relationRules=DeleteDuplicates[Catenate[{First[#]Last[#],Last[#]First[#]}&/@stringRelations]];identityRules=DeleteDuplicates[Catenate[Module[{generator=#},{StringJoin[generator,stringIdentity]generator,StringJoin[stringIdentity,generator]generator}]&/@Join[stringGenerators,{stringIdentity},stringInverses]]];inverseRules=DeleteDuplicates[Catenate[Module[{index=#},{StringJoin[stringGenerators[[#]],stringInverses[[#]]]stringIdentity,StringJoin[stringInverses[[#]],stringGenerators[[#]]]stringIdentity}]&/@Range[Length[generators]]]];ResourceFunction["MultiwaySystem"][Join[generatorRules,relationRules,identityRules,inverseRules],Join[stringGenerators,{stringIdentity},stringInverses],stepCount,rest]]
In[]:=
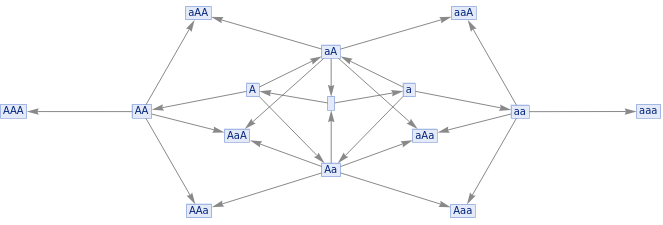
MultiwayGroup[<|"Generators"{"A"},"Relations"{},"Identity""","Inverses"{"a"}|>,2,"StatesGraph"]
Out[]=
[[[ some edges correspond to appending a generator; others to applying a relation ]]]
In[]:=
MultiwayGroup[<|"Generators"{"A"},"Relations"{},"Identity""","Inverses"{"a"}|>,2,"EvolutionEventsGraph"]
Out[]=
In[]:=
MultiwaySemigroup[<|"Generators"{"A"},"Relations"{}|>,2,"StatesGraph"]
Out[]=
In[]:=
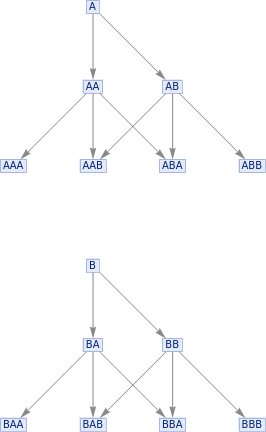
MultiwaySemigroup[<|"Generators"{"A","B"},"Relations"{}|>,2,"StatesGraph"]
Out[]=
In[]:=
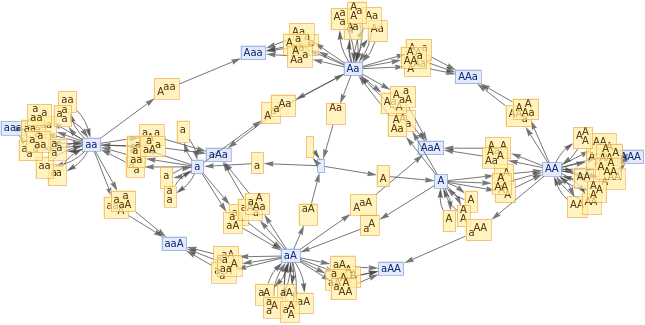
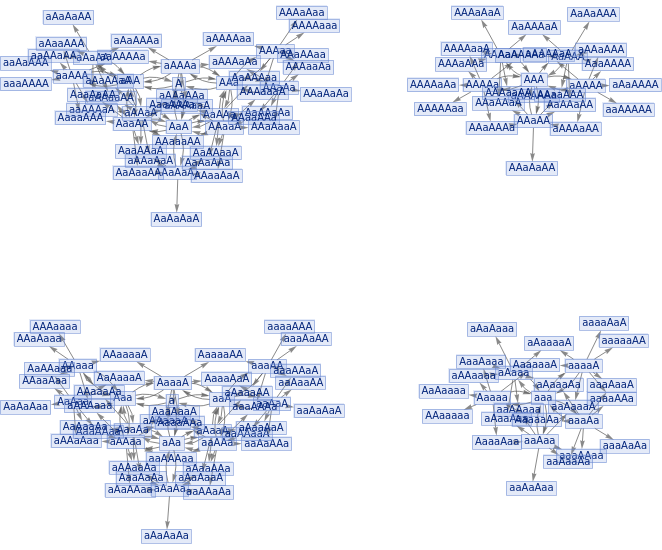
ResourceFunction["MultiwaySystem"][{"Aa""","aA""","""Aa","""aA"},ResourceFunction["StringTuples"]["Aa",3],2,"StatesGraph"]
Out[]=
[[ Should avoid inserting identity elements in the middle of the string ]]
Adding Lemmas
Adding Lemmas
Example of a model: a particular group, vs. groups in general.
One approach: add relations to the generic axioms to force us to have a particular group.
Another approach: explicit multiplication table (i.e. a representation) [there are a set of inequivalent words on which this operates]
One notion of time in a group involves appending generators one at a time [i.e. this is a way to construct an object that corresponds to the group]
One notion of time in a group involves appending generators one at a time [i.e. this is a way to construct an object that corresponds to the group]
Euclid
Euclid
One coordinatization: distance from different common notions
Coordinatization
Coordinatization
Code
Code
More
More
With Novelty Generator
With Novelty Generator
[[ We get this causal invariant structure because we’re adding on both left and right ; but we’d get the same idea by just adding on the right ]]
[[ Hacky approach: just have an X at the end of each string ]]
Free semigroup:
Free semigroup:
Could coordinatize by # of rule applications
[[ Powerful theorem ~ high-mass gravitational lensing object ??? ]]
[[ Powerful theorem ~ high-mass gravitational lensing object ??? ]]
You can add lemmas/relations that give new information
You can add lemmas/relations that give new information
but they have to be consistent with the underlying axiom system
but they have to be consistent with the underlying axiom system
Claim: there is a reasonably uniform coordinatization (or patches) in metamathematical space
Claim: there is a reasonably uniform coordinatization (or patches) in metamathematical space
Leibniz: identity of indiscernables
Mathematics is in practice doable because you can reuse lemmas etc. that you’ve used before
Mathematics is in practice doable because you can reuse lemmas etc. that you’ve used before
We are computationally bounded we build a physics/mathematics that we can do
We are computationally bounded we build a physics/mathematics that we can do
This might not be possible
But it is, because of causal invariance
[causal invariance guarantees we can’t get lost, e.g. doing random search]
How uniformly doable is mathematics?
How uniformly doable is mathematics?
[Is there a systematic way of extracting reducibility from these irreducible systems?]
[Is there a systematic way of extracting reducibility from these irreducible systems?]