A Candidate Geometrical Formalism for the Foundations of Mathematics and Physics
A Candidate Geometrical Formalism for the Foundations of Mathematics and Physics
Formal Correspondences Between Homotopy Type Theory and the Wolfram Model
Formal Correspondences Between Homotopy Type Theory and the Wolfram Model
By Jonathan Gorard (University of Cambridge / Wolfram Research, Inc.)
This bulletin is a writeup of work done in collaboration with Xerxes Arsiwalla and Stephen Wolfram, as publicly presented and discussed in https://www.youtube.com/watch?v=x5v3KFFWv2o.
This bulletin is a writeup of work done in collaboration with Xerxes Arsiwalla and Stephen Wolfram, as publicly presented and discussed in https://www.youtube.com/watch?v=x5v3KFFWv2o.
Introduction
Introduction
The field of “metamathematics” - a term first popularized by David Hilbert in the context of Hilbert’s program to clarify the foundations of mathematics in the early 20th century - may ultimately be regarded as the study of “pre-mathematics”. In other words, while mathematics studies what the properties of particular mathematical structures (such as groups, rings, fields, topological spaces, etc.) may be, metamathematics studies what the properties of mathematics itself, when regarded as a mathematical structure in its own right, are. Metamathematics is thus “pre”-mathematics in the sense that it is the structure from which the structure of mathematics itself develops (much like “pre-geometry” in theoretical cosmology is regarded as the structure from which the structure of the universe itself develops).
In much the same way, the Wolfram Physics Project may be thought of as being the study of “pre-physics”. The Wolfram Model is not a model for fundamental physics in and of itself, but rather an infinite family of models (or, if you prefer, a “formalism”), within which concepts and theories of fundamental physics can be systematically investigated and validated. However, one of the most remarkable things that we have discovered over the year-or-so that we’ve been working on this project is that a shockingly high proportion of the known laws of physics (most notably, general relativity and quantum mechanics) appear to be very “generic” features of the formalism, i.e. they are exhibited by a wide class of models, as opposed to being particular features of our specific universe, as one might otherwise expect. This leads to the tantalizing possibility that, just as metamathematics aims to explain why mathematics has the structure that it does, the Wolfram Model may serve to explain why physics has the structure that it does.
The correspondence between the Wolfram Model and metamathematics goes far deeper than this, though. It does indeed appear that many of the recent innovations in the foundations of mathematics (including dependent type theory, homotopy type theory, the univalence axiom, synthetic geometry, etc.) have considerable overlaps with our recent insights into the foundations of physics (particularly surrounding concepts such as the topology and geometry of rulial space, foliations and fibrations of the rulial multiway system, completion procedures and the inevitability of quantum mechanics, etc.) Indeed, what I aim to sketch out in this bulletin is a potential scheme for a new, computable foundation for both mathematics and physics, which can be thought of as an abstract unification of homotopy type theory and the Wolfram Physics Project.
The Curry-Howard Isomorphism and its Physical Generalization
The Curry-Howard Isomorphism and its Physical Generalization
Let me begin by describing the broad philosophical setup of this bulletin. In mathematical logic and theoretical computer science, there is a famous result named after Haskell Curry and William Alvin Howard (and deeply connected to the core ideas of intuitionistic logic and its operational interpretation) known as the “Curry-Howard isomorphism” or “Curry-Howard correspondence”. Loosely speaking, what it says is that all mathematical proofs can be interpreted as computer programs, and (somewhat more surprisingly), all computer programs can be interpreted as mathematical proofs. In other words, the core problems of proof theory in mathematical logic and programming language theory in theoretical computer science are actually identical.
At some level, the Curry-Howard isomorphism provides the formal justification for an otherwise obvious intuition. In pure mathematics, one starts from a set of “axioms”, one applies a “proof” (in accordance with a set of “rules of inference”), and one obtains a “theorem”. The abstract notion of computation can thus be thought of as being an ultimately desiccated version of the concept of mathematical proof, in which one starts with some “input”, one applies a “computation” (in accordance with a set of “algorithmic rules”), and one obtains an “output”. In other words, one has the formal correspondence:
In[]:=
<|"Axioms""Input","Proof""Computation","Rules of Inference""Algorithmic Rules","Theorem""Output"|>
Indeed, the symbolic nature of the Wolfram Language allows us to see this correspondence explicitly. If we prove a trivial mathematical theorem (such as the theorem that a==c, starting from the axioms that a==b and b==c, i.e. a proof of the transitivity of equality), then we obtain a symbolic proof object:
In[]:=
proof=FindEquationalProof[ac,{ab,bc}]
Out[]=
ProofObject
In[]:=
proof["ProofGraph"]
Out[]=
In[]:=
proof["ProofDataset"]
Out[]=
Each statement in the proof, such as “a==c”, can be interpreted as a symbolic expression. Each application of an inference rule, such as “a->b” (which is, in turn, derived from the axiom “a==b”) can be interpreted as an application of symbolic rewrite rule. Thus, the entire proof can be implemented as a symbolic piece of Wolfram Language code, in which the key steps of the proof are performed using MapAt[...] and Replace[...] functions:
In[]:=
proof["ProofFunction"]
Out[]=
Function[{},Block[{EquationalProof`Axiom,EquationalProof`Hypothesis,EquationalProof`EquationalizedAxiom,EquationalProof`EquationalizedHypothesis,EquationalProof`CriticalPairLemma,EquationalProof`SubstitutionLemma,EquationalProof`Conclusion},=ba;=bc;=ac;=MapAt[Replace[ba],,1];=MapAt[Replace[ac],,FirstPosition[,a]];]]
Axiom
1
Axiom
2
Hypothesis
1
SubstitutionLemma
1
Axiom
2
Conclusion
1
Hypothesis
1
Hypothesis
1
Conclusion
1
Running this piece of code hence allows us to determine that the corresponding theorem is actually true:
In[]:=
proof["ProofFunction"][]
Out[]=
True
As such, we can interpret the Curry-Howard isomorphism as being the statement that every ProofObject in the Wolfram Language has an associated proof function (which we can explicitly demonstrate, as above), and moreover that every piece of symbolic Wolfram Language code has a corresponding interpretation as a ProofObject for some theorem. The latter direction is easy to see once one appreciates that all Wolfram Language programs are ultimately reducible to sequences of transformation operations being applied to symbolic expressions, just like a mathematical proof.
To be a bit more rigorous, the Curry-Howard isomorphism involves using the so-called “Propositions as Types” interpretation of metamathematics; in other words, Curry-Howard states that a program that produces an output of a given data type can be interpreted as a proof that the corresponding type is inhabited, and vice versa.
In the Wolfram Physics Project, and in the field of physics more generally, one also considers an ultimately desiccated notion of what a “physical system” truly is. More specifically, one imagines the system beginning in some “initial state”, undergoing “motion” (in accordance with some “laws of motion”), and ending up in some final state. This immediately suggests a further refinement of the Curry-Howard isomorphism, in which programs, proofs and physical systems are really the same kind of thing:
<|"Initial State""Input","Motion""Computation","Laws of Motion""Algorithmic Rules","Final State""Output"|>
Viewed in this way, the Church-Turing thesis is neither a definition, a theorem nor a conjecture; rather it is a hypothesis of fundamental physics. Namely, what the Church-Turing thesis truly says in this context is that the set of partial functions that can be computed by a universal Turing machine is exactly the set of partial functions that is instantiated by the laws of physics. Or, more concretely, the set of possible motions of a (physically realized) universal Turing machine is in one-to-one correspondence with the set of possible motions of any physical system, anywhere in the universe.
The rest of this bulletin will be dedicated to fleshing out the details and implications of this correspondence, both for the foundations of physics, and for the foundations of math.
Homotopy Type Theory, Univalent Foundations and Synthetic Geometry
Homotopy Type Theory, Univalent Foundations and Synthetic Geometry
Homotopy type theory is an augmentation of type theory (or, more specifically, of Per Martin-Löf’s intuitionistic type theory) with one key additional axiom, namely Vladimir Voevodsky’s axiom of univalence, whose significance we shall discuss later. The key philosophical idea underpinning homotopy type theory is a slight extension of the usual “propositions as types” interpretation of the Curry-Howard correspondence, in which now “types” correspond to topological spaces (homotopy spaces), “terms” of a given type correspond to points in those spaces, proofs of equivalence between terms of a given type correspond to paths connecting the associated points, proofs of equivalence between proofs correspond to (potentially higher) homotopies between the associated paths, etc. In other words, homotopy type theory is a way of endowing type theory (and the foundation of mathematics more generally) with a kind of in-built topological structure.
We know from ordinary topology that, a homotopy is just a continuous deformation between paths. More precisely, given a pair of continuous functions f and g from a topological space X to another topological space Y, one can define a homotopy as being a continuous function h from the product space of X with the (closed) unit interval to Y, where the unit interval can be thought of as “parameterizing” the homotopy. To see this explicitly, suppose that we define function f to just be an ordinary Sin function:
In[]:=
f[x_]:=Sin[x]
In[]:=
Plot[f[x],{x,0,Pi}]
Out[]=
In homotopy type theory, we would interpret this overall space as being a type, the endpoints of this path would be terms of that type, and the path defined by the function f would correspond to the proof that those terms are equivalent. In ordinary mathematics, we are used to the idea that a given theorem can have many (apparently totally different) proofs, such as in the case of the fundamental theorem of algebra, in which there is a great variety of possible proofs stemming from topology, complex analysis, algebra, Riemannian geometry, etc. So suppose now that we define g to be a slightly different function connecting the same two points:
In[]:=
g[x_]:=Sin[x]*Cos[x]
In[]:=
Plot[g[x],{x,0,Pi}]
Out[]=
Now, we can interpret this path as being a different possible proof of the same proposition (namely the proposition that the terms corresponding to the endpoints of the path are equivalent). We can then define a homotopy between these two paths as follows:
In[]:=
h[x_,t_]:=(1-t)*f[x]+t*g[x]
In[]:=
Plot3D[h[x,t],{x,0,Pi},{t,0,1}]
Out[]=
Although this homotopy lives naturally in this higher-dimensional space, we can easily project it back down onto our original space:
In[]:=
Show[Table[Plot[h[x,t],{x,0,Pi},PlotRangeAll],{t,0,1,0.1}]]
Out[]=
Finally, this homotopy can be interpreted as a proof that these two different proofs are actually equivalent (in the sense that they are both valid proofs of the same theorem). As we have now seen explicitly, this homotopy can itself be interpreted as a path in some higher-dimensional space, so we can also proceed to define homotopies between those paths, which would correspond to proofs of equivalence between proofs of equivalence of proofs, etc. Thus, there is really a whole infinite hierarchy of all possible higher-order homotopies, corresponding to the infinite hierarchy of all possible higher-order proofs of equivalence, and this hierarchy will becomes relevant soon, once we start considering its implications for the geometry of rulial space.
The effort to formalize mathematics in terms of homotopy type theory is commonly known as the “univalent foundations program”, in reference to the central role played by Voevodsky’s univalence axiom. One of the “big picture” questions driving the advancement of univalent foundations (as well as many related areas, such as Michael Shulman’s formulations of “synthetic topology”, “cohesive geometry”, etc.) is a desire to better understand the role of “space” in the foundations of mathematics.
In many ways, it is a great mystery why so many different mathematical structures (such as groups, rings, fields, Boolean algebras, lattices, etc.) also come equipped with a corresponding notion of “space”. For instance, in the context of group theory, a group is usually defined purely algebraically (i.e. as a closed algebraic structure obeying the axioms of associativity, identity and inverse), and yet one nevertheless has Lie groups, topological groups, matrix groups, loop spaces, etc., within all of which there naturally appears some corresponding spatial structure (such as a differentiable manifold in the case of a Lie group, or a topological space in the case of a topological group, etc.), which seems to “come along for the ride”, in the sense that the spatial structure is somehow respected by all of the underlying algebraic operations.
We can see this explicitly by considering the case of the Lie group SO(3). First, consider the set of all 3x3 matrices of determinant 1; here, we shall look directly at a finite subset:
Then, SO(3) can be defined purely syntactically in terms of a binary operation on this set of elements (in this case, corresponding to matrix multiplication) that obeys the axioms of associativity:
identity:
and inverse:
However, because of the interpretation of 3x3 matrices of determinant 1 as 3D rotation matrices, SO(3) comes naturally equipped with a spatial structure corresponding to the following differentiable manifold (and, hence, is indeed a Lie group):
But why? The ZFC axioms of set theory are purely syntactical and algebraic: there is no inherent notion of “space” in ZFC. So why should objects (like groups) defined within ZFC in a purely syntactical and algebraic way induce a notion of space as if by magic? Homotopy type theory aims to address the mystery of the origin of space, by considering instead a foundation for mathematics that is explicitly spatial and topological at the outset, and in which the syntactical structure of mathematics is somehow emergent.
In the context of the Wolfram Physics Project, we found ourselves addressing a very similar question. Our models are defined purely combinatorially, in terms of replacement operations on set systems (or, equivalently, in terms of transformation rules on hypergraphs). And yet, the correspondence between our models and known laws of physics depends upon their being a reasonable interpretation of these combinatorial structure in terms of continuous spaces. Our derivation of the Einstein field equations, for instance, depends upon spatial hypergraphs having a reasonable continuum limit in terms of Riemannian manifolds (and hence being a reasonable candidate for physical space):
And, moreover, it depends upon causal graphs having a reasonable continuum limit in terms of Lorentzian manifolds (and hence being a reasonable candidate for spacetime):
And, at a more abstract and speculative level, some of our current conjectures regarding the quantum mechanical aspects of our formalism depend upon the continuum limit of branchial graphs in multiway systems as being projective Hilbert spaces:
Or multiway causal graphs as being twistor correspondence spaces:
So could these two questions be related? Could the explanations offered by homotopy type theory for the origins of spatial structure in mathematics also imply, after appropriate translation, equivalent explanations for the origins of spatial structure in physics? And if so, what would the things we’ve discovered in the course of the Wolfram Physics Project so far imply regarding the foundations of mathematics?
Multiway Systems as Models for Homotopy Type Theory
Multiway Systems as Models for Homotopy Type Theory
As discussed above, the axioms of a mathematical theory can be interpreted as defined transformation rules between symbolic expressions. For instance, in the axioms of group theory:
The associativity axiom can be interpreted as the following pair of (delayed) pattern rules:
Therefore, a proof of a mathematical proposition can ultimately be represented as a multiway system. Indeed, at some level, this is precisely what a ProofObject is:
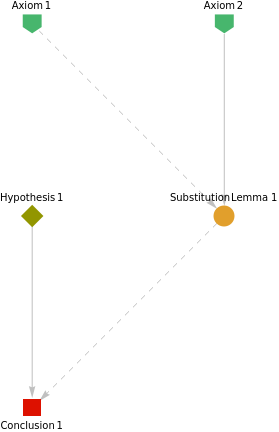
A ProofObject is formatted a little differently to the way multiway systems are conventionally formatted. The green (downwards-pointing) arrows are the axioms, the turquoise diamond is the hypothesis and the red square is the conclusion (in this case, the conclusion being that the hypothesis is true). Each of the orange circles is a substitution lemma, and can be thought of as an ordinary multiway state node: it’s an intermediate lemma that is deduced along the way by simply applying the axiomatic transformation rules described above, just like in a regular multiway system. However, each of the dark orange triangles is a critical pair lemma, which is an indication of a place where the multiway system bifurcates, and in which an additional lemma is necessary in order to prevent it from doing so (in other words, it corresponds to a place where a completion procedure has been applied). Looking at a specific example:
Here, we see that two rules, indicated by “Rule” and “MatchingRule” (derived from Axiom 2 and Axiom 1, respectively) both match a common subpattern, indicated by “Subpattern”, thus producing a bifurcation in the multiway system. However, since both elements of the bifurcation were derived from a common expression by valid application of the rewrite rules, this bifurcation itself constitutes a proof that the elements are equivalent, and hence we can declare them to be equal (which is the critical pair lemma). This declaration of equivalence immediately forces the bifurcation to collapse, so by adding a sufficient number of critical pair lemmas to the rewrite system, we can therefore force the multiway system to have only a single path (up to critical pair equivalence). This, incidentally, is identical to the process of adding critical pair completions so as to force causal invariance, which is the basis of our current model for quantum measurement; the correspondence with quantum mechanics will be explored in more detail later.
Therefore, the proof graph can be thought of as being an intermediate between a single evolution thread and a whole multiway system; the substitution lemmas by themselves indicate the path of a single evolution thread, but the critical pair lemmas indicate the places where that evolution thread has been “plumbed into” a large, bifurcating multiway system. We can see this correspondence more directly by considering a simple string multiway system:
We can clearly see that the strings “AA” and “ABBBABBB” are connected by a path in the multiway system - a fact that we can visualize explicitly:
In effect, we can interpret this path as being a proof of the proposition that “AA”->”ABBBABBB”, given the axiom “A”->”AB”. To make the correspondence manifest, with a small amount of additional code we can also represent this path directly as a ProofObject:
Of course, a key idea in homotopy type theory is that we can consider the existence of multiple paths connecting the same pair of points, and hence multiple proofs of the same proposition. For instance, take:
Homotopy type theory then tells us that we can represent the proof of equivalence of these proofs as a homotopy between the associated paths. Since an (invertible) homotopy is ultimately just a mapping from points on one path to corresponding points on the other path (and back again), this is easy to represent discretely:
However, this homotopy is kind of a “fake”, in the sense that it has been explicitly grafted on to the multiway system after-the-fact. The more “honest” way to enact a homotopy of this kind would be to define explicit multiway rules mapping from states along one path onto states along the other, thus yielding:
As Xerxes Arsiwalla pointed out, it is therefore correct to think of the multiway rules (like “A”->”AB”) as being analogous to type constructors in mathematical logic (i.e. rules for building new types), so as to allow the multiway systems themselves to be interpreted as inductive types, just as homotopy type theory requires. Moreover, these completion procedures described above that allow us to define homotopies between paths are a kind of higher-order rule (i.e. they are rules for generating new rules), with the result being that the higher-dimensional multiway system that one obtains after applying such a completion procedure is the analog of a higher inductive type. Since there exists an infinite hierarchy of higher inductive types, it follows that there must exist a corresponding infinite hierarchy of higher-order multiway systems, with the multiway system at level n being a partially “completed” version of the multiway system at level n-1 (i.e. in which certain explicit homotopies have been defined between certain pairs of paths). So a natural question to ask is: what kind of mathematical structure would such a hierarchy represent?
Groupoids, Topoi and Grothendieck’s Hypothesis
Groupoids, Topoi and Grothendieck’s Hypothesis
A “category” is just a collection of objects (which can be represented as nodes), along with a collection of “morphisms” between those objects (which can be represented as directed edges), and with the property that all morphisms are both associative and reflexive (i.e. there exists an identity morphism for each object). For instance, starting from a directed graph:
We can force every directed edge (i.e. morphism) to be associative by computing the transitive closure:
And then we can enforce reflexivity by adding a self-loop (i.e. an identity morphism) for each vertex:
Thus, this directed graph has a bona fide interpretation as a small category (small because the corresponding directed graph is finite). On the other hand, a “groupoid” is a special case of a category in which all morphisms are invertible (and hence are isomorphisms), which we can again demonstrate purely graph-theoretically by converting our directed graph into an undirected one:
Or, to be even more explicit, we could add two-way directed edges to indicate isomorphisms:
Groupoids are so named because they generalize ordinary algebraic groups; a group can essentially be thought of as a special case of a groupoid that contains just a single object, and where the invertible morphism corresponds to the (unary) group inverse operation.
Closely related to groupoids are objects known as “topoi”, which can be thought of as being the abstract categorical generalization of point set topology. A “topos” is a category that “behaves like” the category of sets (or, to be more precise, like the category of sheaves of sets on a given topological space) in some suitably defined sense. The crucial feature of a topos that relates it to a groupoid, however, is that topoi necessarily possess a notion of “localization”.
In ordinary commutative algebra, rings are not required to possess multiplicative inverses for all elements, so one can “localize” the ring by introducing denominators (such that the localization is like a restricted version of the field of fractions), thereby introducing multiplicative for elements where they did not previously exist. Similarly, the localization of a category introduces some inverse morphisms where they did not previously exist, hence converting some morphisms into isomorphisms, and thus causing the category to behave “locally” like a groupoid. All of our multiway systems are naturally equipped with a notion of localization; for instance, consider the string multiway system we explored earlier:
We can now select 10 edges at random and introduce their reverse directed edges, to simulate adding inverse morphisms for a collection of ten random morphisms.
Much like in the foliation example given above, this method of localization is kind of a “fake”, since we are artificially grafting these inverted edges onto a pre-existing multiway graph. Instead, we can simply adjoin the reversed edges as new set of multiway rules:
Applying this localization procedure to the entire multiway rule, unsurprisingly, yields the following groupoid-like structure:
Since, in the category of sets, all objects are sets and all morphisms are functions from sets to sets, because for any function from set A to set B there can exist (at least locally) an inverse function from set B to set A, the category of sets is trivially localizable. It is in this sense that we can say that more general topoi “behave like” the category of sets.
One can make this correspondence more mathematically rigorous by realizing (as noted by Xerxes) that, when interpreting multiway systems as inductive types and the associated multiway rules as type constructors, then so long as one includes a “subobject classifier” (where a special object in the category that generalizes the notion of a subset identifier, where all subobjects of a given object in the category correspond to morphisms from the subobject onto the subobject classifier), and assuming that finite limits exist (where a limit is a categorical construction that generalizes the universal constructions of products and pullbacks), the resulting multiway system that one obtains is precisely an elementary topos. We have furthermore made the conjecture (although we do not yet know how to prove it) that this subobject classifier is what endows our multiway systems with a concept of “foliation” that is so crucial for constructing branchial spaces, and for deducing both quantum mechanics and general relativity in the appropriate continuum limits, since at least intuitively each hypersurface in the foliation may be thought of as corresponding to a subobject in the corresponding category. We shall explore this conjecture more closely, and examine precisely what foliations of multiway systems mean from a metamathematical standpoint, within the next section.
For the time being, however, it suffices to realize that such an elementary topos comes naturally equipped (thanks to various results in cohesive geometry) with a functor (that is, a map between categories) to the topos of sets, as well as a pair of adjoint functors (where adjunction here refers to a kind of “weak” equivalence relation) admitting the discrete and indiscrete topologies, respectively. Free topoi possessing this particular collection of functors provide a means of formalizing the notion of a topological space.
Gauge-Dependence of Mathematical Truth and a “Relativistic” Interpretation of the Incompleteness Theorems
Gauge-Dependence of Mathematical Truth and a “Relativistic” Interpretation of the Incompleteness Theorems
Kurt Gödel’s proof of the incompleteness theorems in 1931 established, via the ingenious technique of Gödel numbering, that Peano arithmetic (the standard axiom system for integer arithmetic) was capable of universal computation. Therefore, in particular, he demonstrated that Peano arithmetic could be set up so as to encode the statement “This statement is unprovable.” as a statement about natural numbers. Clearly, if this statement is true, then it is unprovable (so Peano arithmetic is incomplete), and if it is false, then it is provable (so Peano arithmetic is inconsistent).
As such, one way to phrase the first incompleteness theorem is that “If Peano arithmetic is consistent, then there will exist propositions that are independent of the Peano axioms.” In other words, there will exist propositions where neither the proposition nor its negation are (syntactically) provable using the axioms of Peano arithmetic in any finite time.
Notes / To-Do
Completions (i.e. quantum mechanics) are applications of the univalence axiom.
Ability to perform quantum measurement is a statement of multiway topology (not too much “branchiness”).
Mystery: Define something set-theoretically, often a space “appears”. Why?
Define a causal network, often a spacetime “appears”.
Define a causal network, often a spacetime “appears”.
ZFC: Axiom of Extensionality - like “completions” in set theory.
It’s a StateEquivalenceFunction for set theory.
It’s a StateEquivalenceFunction for set theory.
Ultimate nature of mathematics/physics: Things that can be considered equivalent can also be considered identical.
“Cayley Graph” of a multiway system is an “infinitely completed” states graph (JG conjecture: this is a groupoid.)
Axiom of Extensions/Univalence/etc. are byproducts of us as observers choosing to model mathematics in the same way we model physics.
Ability to do mathematics arises in the same way as ability to understand physics (the existence of computational reducibility/rulial black holes/etc.)
Ability to do mathematics arises in the same way as ability to understand physics (the existence of computational reducibility/rulial black holes/etc.)
Xerxes: “Conventional” uncertainty principle is a limit on what can be measured in physics.
This formalism is constructivist by nature (because of univalence, so no axiom of choice, no law of excluded middle, etc.), so there are limits on what can be constructed in mathematics. Is this the uncertainty principle?
This formalism is constructivist by nature (because of univalence, so no axiom of choice, no law of excluded middle, etc.), so there are limits on what can be constructed in mathematics. Is this the uncertainty principle?
Grothendieck’s Hypothesis: All infinity-groupoids are topological (homotopy) spaces.
Groupoids: A category in which all morphisms are isomorphisms.
Topos: A category that “behaves like” the category of sets (i.e. “Set”).
More precisely, a category that possesses a “localization” notion.
(Analogy to commutative algebra: ring localization introduces denominators.)
More precisely, a category that possesses a “localization” notion.
(Analogy to commutative algebra: ring localization introduces denominators.)
First incompleteness theorem: If PA/ZFC is consistent, there exist propositions that are independent of PA/ZFC, i.e. propositions where neither it nor its negation are syntactically provable (in finite time).
(Proof-theoretic statement)
CH is independent of ZFC => There exist models of ZFC such that ZFC+CH is consistent <=> ZFC is consistent (Godel), and models such that ZFC+CH is inconsistent (Cohen, forcing).
(Model-theoretic implication)
(Proof-theoretic statement)
CH is independent of ZFC => There exist models of ZFC such that ZFC+CH is consistent <=> ZFC is consistent (Godel), and models such that ZFC+CH is inconsistent (Cohen, forcing).
(Model-theoretic implication)
First incompleteness theorem (WPP): Gauge-dependence in mathematics.
Proof theory: Defines a partial order on mathematics.
Model theory: Gauge choice that allows one to construct a total order.
Model theory: Gauge choice that allows one to construct a total order.
Ordinary relativity: There is a causal partial order (conformal structure of spacetime).
Timelike ordering is gauge-invariant, spacelike is gauge-dependent.
There exist propositions (defined by proof theory) whose truth is gauge-invariant (syntactically provable), and those (defined by model theory) whose truth is gauge-dependent.
Timelike ordering is gauge-invariant, spacelike is gauge-dependent.
There exist propositions (defined by proof theory) whose truth is gauge-invariant (syntactically provable), and those (defined by model theory) whose truth is gauge-dependent.
Non-constructive proofs are like boundaries of light cones (proofs that travel “at the speed of proof”), so cannot be witnessed by any “subliminal” model.
Black holes are like “inevitable non-constructivism” in mathematics.
=> (Axiom of Choice is a black hole?)
Black holes are like “inevitable non-constructivism” in mathematics.
=> (Axiom of Choice is a black hole?)
SR: Model-independence of proof theory (syntactically provable statements).
=> A model-theoretic speedup theorem (analog of Lorentz transformation).
=> A model-theoretic speedup theorem (analog of Lorentz transformation).
Inertial frames: “Free” models? (Look this up...)
Superposition in QM: There exists proof redundancy.
Godel’s speed-up theorem: “This statement is unprovable using fewer than n symbols.” (takes n symbols to prove in PA, but is trivial to prove in PA+Con(PA).)
For any pair of propositions, determining whether there exists a path between them may take an arbitrarily large amount of computational effort.
(Defining truth/falsehood in terms of consistency/inconsistency with the total/partial order.)
(Syntactical truth is consistency with partial order, semantic truth is consistency with model-induced total order.)
(Defining truth/falsehood in terms of consistency/inconsistency with the total/partial order.)
(Syntactical truth is consistency with partial order, semantic truth is consistency with model-induced total order.)
General relativity: what is the name for timelike geodesics that are so long that the endpoints appear to be spacelike-separated?
* timelike singularity!! *
* timelike singularity!! *
Connection to Malament-Hogarth spacetimes?
Mathematics is partially ordered, because mathematicians are computationally bounded?
Propositional extensionality (logic): If propositions are path-connected then they are defined to be “equivalent”.
Voevodsky’s Univalence Axiom: (If propositions are equivalent, then they are defined to be “identical”.) <- This implication is itself an equivalence.
Voevodsky’s Univalence Axiom: (If propositions are equivalent, then they are defined to be “identical”.) <- This implication is itself an equivalence.
(Xerxes): Take a multiway system, include a subobject classifier (the categorical analog of a subset identifier) as one of the type constructors, then you get an elementary topos (assuming that finite limits exist).
Interpretation of the Schwarzschild radius: There is a limit to the height of the “abstraction tower” that you can build in mathematics whilst still being a bona fide constructivist.
Increased “abstraction” (energy-momentum in “proof space”), there is gravitational lensing, creating more inequivalent proofs of the same propositions.
i.e. abstraction => (proof-theoretic) redundancy.
i.e. abstraction => (proof-theoretic) redundancy.
(Conjecture): Subobject classifiers allow you to define foliations.
(Xerxes): Such an elementary topos comes naturally equipped with a functor from the topos to the topos of sets, as well as a pair adjoint functors admitting the discrete and indiscrete topologies.
Free (and local) topoi with this collection of functors formalize the notion of a topological space.
=> Locality comes from the subobject classifier, and hence from the “locality” of foliations.
Free (and local) topoi with this collection of functors formalize the notion of a topological space.
=> Locality comes from the subobject classifier, and hence from the “locality” of foliations.
Fibration: Formalization of the idea that you can parameterize one topological space (fibre) with another one (base).
Connection: A rule allowing you to “lift” a step in the base space to a step in the fibre.
Fibration relaxes ordinary fibre bundle, since fibres don’t have to be in the same topological space (or indeed homeomorphic); you just need homotopy-equivalence (i.e. the “homotopy lifting property”).
Connection: A rule allowing you to “lift” a step in the base space to a step in the fibre.
Fibration relaxes ordinary fibre bundle, since fibres don’t have to be in the same topological space (or indeed homeomorphic); you just need homotopy-equivalence (i.e. the “homotopy lifting property”).
Categorical Quantum Mechanics (Abramsky and Coecke): Symmetric monoidal category.
Monoidal category: Category equipped with a tensor product on objects.
Symmetric monoidal category: Monoidal category where the product is “as commutative possible”.
Monoidal category: Category equipped with a tensor product on objects.
Symmetric monoidal category: Monoidal category where the product is “as commutative possible”.
(Xerxes): So long as we have a tensor product constructor, we recover categorical QM upon foliating the rulial multiway system.