In[]:=
HighlightGraph[ResourceFunction["MultiwaySystem"]["A""AB","AA",8,"StatesGraphStructure",EpilogstraightFoliationLines[{1,0},{0,0},#&,{0,0}]],{"ABBA","ABABBB"}]
Out[]=
Models based on transfinite ordinals define foliations in “higher-order” (rulial) multiway systems. (Did Turing discover rulial space by accident?)
Simultaneity is an equivalence relation.
“Spacelike hypersurfaces” are sets of mutually independent (i.e. semantic truth values are undefined) propositions with respect to the model.
"Spatial motion” is defining new sets of equivalences between such propositions.
In[]:=
HighlightGraph[ResourceFunction["MultiwaySystem"]["A""AB","AA",8,"StatesGraphStructure",EpilogstraightFoliationLines[{1,0},{0.5,0},#&,{0,0}]],{"ABBA","ABABBB"}]
Out[]=
A pair of points is “spacelike-separated” if they correspond to a proposition that is independent of the axioms.
A “free model” is one that is defined by a single equivalence, because it has a single generator (that equivalence), and no additional relations. These correspond to inertial frames (SW: should be renamed “inertial models”).
Maximal non-freedom is a “full” total order.
=> There should be an analog of Godel’s slowdown theorem for model theory.
Proof-theoretic Minkowski metric: positive eigenvalue associated with model verification time, negative eigenvalue associated with proposition verification time.
Lorentz symmetry: Proof-theoretic Minkowski metric is invariant (i.e. any gains in computational efficiency of proof verifications are offset by losses in computational efficiency of model verification).
Lorentz symmetry: Proof-theoretic Minkowski metric is invariant (i.e. any gains in computational efficiency of proof verifications are offset by losses in computational efficiency of model verification).
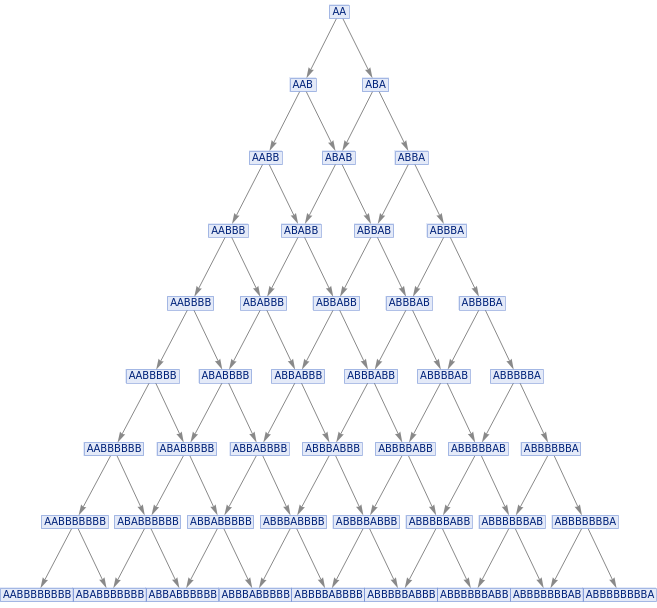
In[]:=
ResourceFunction["MultiwaySystem"]["A""AB","AA",8,"StatesGraph"]
Out[]=
In[]:=
path1=FindShortestPath[mwGraph,"ABAB","ABABBBBBBB"]
Out[]=
{ABAB,ABABB,ABABBB,ABABBBB,ABABBBBB,ABABBBBBB,ABABBBBBBB}
In[]:=
path2=FindShortestPath[mwGraph,"ABAB","ABBBBBBBAB"]
Out[]=
{ABAB,ABBAB,ABBBAB,ABBBBAB,ABBBBBAB,ABBBBBBAB,ABBBBBBBAB}
In[]:=
futureLightCone=VertexOutComponent[mwGraph,"ABAB"]
Out[]=
{ABAB,ABABB,ABBAB,ABABBB,ABBABB,ABBBAB,ABABBBB,ABBABBB,ABBBABB,ABBBBAB,ABABBBBB,ABBABBBB,ABBBABBB,ABBBBABB,ABBBBBAB,ABABBBBBB,ABBABBBBB,ABBBABBBB,ABBBBABBB,ABBBBBABB,ABBBBBBAB,ABABBBBBBB,ABBABBBBBB,ABBBABBBBB,ABBBBABBBB,ABBBBBABBB,ABBBBBBABB,ABBBBBBBAB}
In[]:=
mwGraph=ResourceFunction["MultiwaySystem"]["A""AB","AA",8,"StatesGraphStructure"]
Out[]=
In[]:=
HighlightGraph[mwGraph,Subgraph[mwGraph,futureLightCone]]
Out[]=
Non-constructive propositions correspond to the boundaries of elementary proof cones (because they correspond to timelike paths); constructive propositions correspond to the interiors of the same cones.
Model-theoretic gerrymandering may be related to inability to construct things like Malament-Hogarth spacetimes (i.e. in both cases, hypercomputation would be required on the part of the “observer”).
In standard group presentation theory, one makes a distinction between generators and relations. Here, we don’t need to do this (group generators just correspond to unidirectional multiway rules, )
A model “moving along a timelike path” is not-constructible, because constructing/verifying it would require infinite computational effort.
Propositional independence <=> linear independence.
Objective reality in mathematics is causal invariance induced by the univalence axiom. Objective reality in quantum mechanics is causal invariance induced by measurement.
Measurement is “applied univalence”.
Measurement is “applied univalence”.
The first incompleteness theorem is the analog of the strong cosmic censorship conjecture.
A Cauchy surface in relativity: a collection of spacelike-separated points such that every timelike null vector intersects the surface exactly once.
Within reasons, models can simulate strong axiom systems (but you are still computationally bounded, so no free lunch).
Riemann curvature in GR <=> uncertainty principle in QM <=> critical pairs in automated theorem-provers
(One is non-commutativity of covariant derivatives, one is non-commutativity of measurement operators, one is non-commutativity of inferences.)
(One is non-commutativity of covariant derivatives, one is non-commutativity of measurement operators, one is non-commutativity of inferences.)
Curvature in proof space is witnessed by the density of critical pair lemmas (elementary holonomies, from which the “Riemann curvature tensor” can be derived). We see this explicitly by seeing a nontrivial relationship between a perturbation of a geodesic and its length.
Claim: The greater the dependence upon previous results, the more creativity is required to prove theorems (because there’s greater choice of things to do...)
The more mathematical tools you know, the more you can go off track (if you can only do one thing, you either prove the theorem or you don’t, etc.)
Energy-momentum as dependence on prior results (just as energy-momentum as Lagrangian density in QM) behaves more like vacuum energy than baryonic matter (obvious claim, because we aren’t considering topological obstructions, yet!!)
QM Stuff
QM Stuff
Functor maps from one category to another. Bifunctor maps from two categories to one.
Category Quantum Mechanics (Coecke and Abramsky): QM can be done in a symmetric monoidal category (i.e. a category equipped with bifunctor interpreted as a tensor product, with an additional left- and right-identity object for the bifunctor, and where this bifunctor is as commutative as possible).
Generalized tensor product spaces are concatenations of multiway rules.
In categorical quantum mechanics, we use only planar diagrams.
These branchial graphs are “thin” in the sense that they only respect branchial ancestry up a single level.
If we produced a “thickened” branchial graph, respecting branchial ancestry up multiple levels, it would be natural to represent using hyperedges (because there will be multiple ancestors) => Branchial hypergraphs.
(Xerxes): This is a more general tensor product construction than one would consider in symmetric monoidal category theory.
If we produced a “thickened” branchial graph, respecting branchial ancestry up multiple levels, it would be natural to represent using hyperedges (because there will be multiple ancestors) => Branchial hypergraphs.
(Xerxes): This is a more general tensor product construction than one would consider in symmetric monoidal category theory.
Univalence and Stuff
Univalence and Stuff
Foliations and fibrations are equivalent (JG claim).
We can simulate fibration of (e.g.) a rulial multiway system down to a particular multiway system by just defining equivalences that collapse all branches that aren’t the multiway system we care about down to the multiway system that we do (i.e. a foliation).
=> Fibrations can be achieved by performing completions.
The “fibrations as foliations” interpretation is claiming that when a pair of states are equivalent (by virtue of a foliation / choice of completion rules / etc.), then they can be treated as identical.
This is precisely the statement of univalence.
This is precisely the statement of univalence.
Causal invariance, univalence and “completability” are equivalent (up to some extensionality axiom...)
“StateEquivalenceFunction” in a multiway system is defining a notion of logical extensionality.
Human mathematics depends upon computational reducibility, and computational reducibility is all about “throwing away the intermediate computational effort”.
Proofs are an “excuse” to care only about the theorem, without repeating the logic of the proof in subsequent computations.
“It’s all about the journey, man.” -Physicists
Mathematicians care only about the destination.
Mathematicians care only about the destination.
Critical pair lemmas are defining colinearity of terms.
The homotopies in rulial space endow it with a spatial structure, which is then inherited by all lower-order objects (including, e.g. Hilbert space, spacetime, physical space, etc.)
Space: Set endowed with “some additional structure”.
Circular definition of space: Any feature that is inherited from weak homotopy equivalence in the infinity-groupoid.
Can you have a space with only a trivial topology?
Immediate To-Dos
Immediate To-Dos
Write code to convert between multiway systems and proof objects.
Empirical of proof objects using FindEquationalProof, attempting to determine the analog of the Einstein field equations (i.e. the relationship between critical pair lemma density and causal edge density (in particular directions)).
What are topological obstructions in proof space (or, for that matter, in rulial/branchial space, etc.)?
(More general) Investigate hypergraphs as a way of representing thickened branchial graphs.
Conjecture about Topological Obstructions
Conjecture about Topological Obstructions
Interpret topology of rulial space as computability theory, interpret (induced) geometry as computational complexity theory.
Reducibility of one complexity class to another is a diffeomorphism of some description (probably quasiconformal).
=> Topological obstructions are the complete problems (e.g. NP-complete problems), which prevent such a diffeomorphism from being constructed.
By Curry-Howard, proofs are program syntax, models are program semantics. Therefore, we can discuss “complexity classes” of models.
Path integral in the space of possible programs is weighted both by the maximum speed of simulation, and by the number of “redundant” programs (i.e. programs that produce the same semantic behavior from different syntactical structure).
Bottom line: We can “computational complexify” model theory.