Hard Spheres Simulation for Stephen Wolfram –– Trajectories and Collisions
Hard Spheres Simulation for Stephen Wolfram –– Trajectories and Collisions
Matt Kafker
September,2020
September
th
26
Hard Spheres Simulation: Returns Trajectories and Collisions
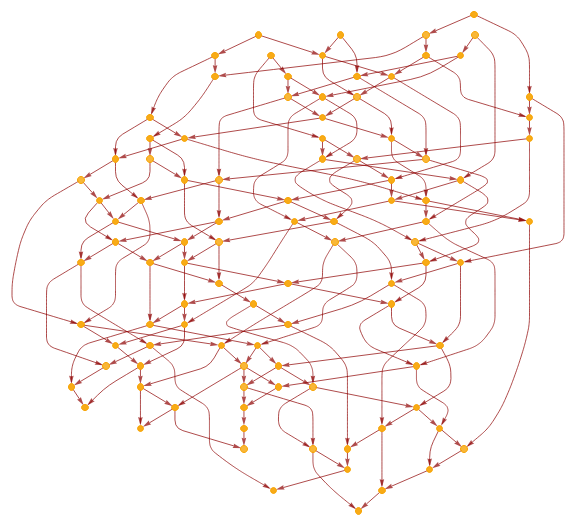
Generate Causal Graph from Collisions
Visualization
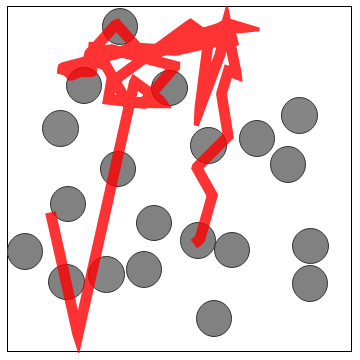
Visualize 2D simulation with randomly distributed initial conditions. (Mostly included as a sanity check.)
Now draws tail of specified particle.
Now draws tail of specified particle.
In[]:=
visualize2D[num_,steps_,boxSize_,trackedParticle_]:=Module[{initialConditions,traj,stepSize=.1,rad=1},(*Changeseedfordifferentbehavior!*)SeedRandom[1234];(*Randomlydistributedpositionswithrandomlydistributedvelcities*)initialConditions=N[{RandomReal[{-#,#}&@(boxSize-rad),{num,2}],RandomPoint[Ball[ConstantArray[0,2]],num]}];(*Simulateabox,animatetheresults*)traj=simulateCollisionsBox[initialConditions,N[boxSize],N[stepSize],N[rad],steps]〚1,All,1〛;Animate[Graphics[{{FaceForm[],EdgeForm[Black],Rectangle[{-boxSize,-boxSize},{boxSize,boxSize}]},Style[Disk[#,rad]&/@traj〚All,t〛,Gray,EdgeForm[GrayLevel[.2]]],(*drawtailofparticle*)Style[Line[traj[[trackedParticle,;;t]]],Red,Thickness[0.03],Opacity[0.8]]}],{t,1,Length[traj〚1〛],1},DefaultDuration8,SaveDefinitionsTrue]];
Sample visualization.
In[]:=
visualize2D[20,2000,10,2]
Out[]=
In[]:=
?SeedRandom
Out[]=
More (SW) ...
More (SW) ...
In[]:=
SeedRandom[1234];hscg=Graph[ResourceFunction["WolframPhysicsProjectStyleData"]["CausalGraph"]["Function"][genCausalGraph[20,500,10,2]],AspectRatio.9]
Out[]=
In[]:=
trajectories2D[num_,steps_,boxSize_]:=Module[{initialConditions,traj,stepSize=.1,rad=1},(*Changeseedfordifferentbehavior!*)SeedRandom[1234];(*Randomlydistributedpositionswithrandomlydistributedvelcities*)initialConditions=N[{RandomReal[{-#,#}&@(boxSize-rad),{num,2}],RandomPoint[Ball[ConstantArray[0,2]],num]}];(*Simulateabox,animatetheresults*)traj=simulateCollisionsBox[initialConditions,N[boxSize],N[stepSize],N[rad],steps]〚1,All,1〛]
In[]:=
trajectories2D[20,500,10]
Out[]=
In[]:=
Dimensions[%]
Out[]=
{20,501,2}
In[]:=
SortBy[VertexOutComponent[hscg,{SortBy[VertexList[hscg],Last][[25]]}],Last]
Out[]=
{{7,5,215},{5,2,227},{7,2,255},{13,2,258},{13,9,272},{13,7,273},{5,3,276},{4,2,285},{14,3,296},{14,4,300},{5,2,313},{13,4,313},{20,13,324},{20,19,334},{14,2,342},{13,4,345},{6,4,354},{14,13,361},{20,12,363},{7,2,375},{13,10,375},{10,1,378},{18,9,380},{7,2,383},{18,2,391},{19,8,395},{17,4,397},{20,13,400},{10,8,413},{13,10,413},{10,8,414},{10,8,415},{20,7,418},{12,7,428},{9,7,431},{17,6,442},{5,3,443},{20,13,443},{18,9,444},{5,2,449},{5,3,450},{19,12,460},{14,3,463},{19,16,464},{19,12,468},{11,6,476},{12,7,482},{11,1,484},{20,18,484},{11,6,486},{8,1,489},{18,2,493},{17,14,494},{13,12,500}}
In[]:=
trajectories2D[20,500,10][[All,375]]
Out[]=
{{-2.96385,-3.03663},{1.9927,8.6016},{-7.47853,5.24821},{-4.8009,2.24495},{-7.15252,8.88814},{-4.96696,-0.660656},{3.22016,7.01409},{2.19223,-3.89441},{8.14118,6.90435},{-1.10217,-1.7535},{-5.65462,-2.76155},{7.4745,2.11644},{-0.244738,0.136836},{-1.95596,3.28807},{-1.82262,-8.37062},{1.4865,-8.92225},{-8.53132,2.03519},{6.27504,8.49987},{7.90079,-2.27051},{4.75838,1.29956}}