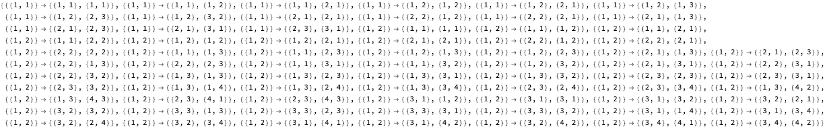EnumerateWolframModelRules[{{1,2}}{{2,2}}]
In[]:=
Out[]=
GatherBy[ParallelMapMonitored[{WolframModelTest[#,Automatic]["Sizes"],#}&,%],First];
In[]:=
First/@%
In[]:=
Out[]=
EnumerateWolframModelRules[{{1,2}}{{3,2}}];
In[]:=
GatherBy[ParallelMapMonitored[{WolframModelTest[#,Automatic]["Sizes"],#}&,%],First];
In[]:=
First/@%
In[]:=
Out[]=
$PhysicsDataDirectory
In[]:=
/Users/sw/Dropbox/Physics/Data
Out[]=
allrules=Import["/Users/sw/Dropbox/Physics/Data/RuleEnumerations/12-42c.wxf"];
In[]:=
GatherBy[ParallelMapMonitored[{WolframModelTest[#,Automatic]["Sizes"],#}&,allrules],First];
In[]:=
First/@%
In[]:=
Out[]=
First/@%
In[]:=
Out[]=
FindLinearRecurrence/@%
In[]:=
{{4},{-1,17},{-1,14},FindLinearRecurrence[{1,4,13,40}],FindLinearRecurrence[{1,4,10,22}],{2,-1},{3,-2},{2,-1},{2,-1},{1},{2,-1},{4,-3},{4}}
Out[]=
Length/@WolframModel[{{1,1}}{{1,1},{1,1},{1,2},{2,2}},{{0,0}},8,"StatesList"]
In[]:=
{1,4,13,40,121,364,1093,3280,9841}
Out[]=
FindLinearRecurrence[%]
In[]:=
{4,-3}
Out[]=
allrules=Import["/Users/sw/Dropbox/Physics/Data/RuleEnumerations/13-23c.wxf"];
In[]:=
GatherBy[ParallelMapMonitored[{WolframModelTest[#,Automatic]["Sizes"],#}&,allrules],First];
In[]:=
First/@%
In[]:=
Out[]=
First/@%
In[]:=
Out[]=
FindLinearRecurrence/@%
In[]:=
Out[]=
{{1,2,1}}{{1,1,2},{2,3,2}}
allrules=Import["/Users/sw/Dropbox/Physics/Data/RuleEnumerations/22-32c.wxf"];
In[]:=
GatherBy[ParallelMapMonitored[{WolframModelTest[#,Automatic]["Sizes"],#}&,allrules],First];
In[]:=
First/@%
In[]:=
Out[]=
{FindLinearRecurrence[#[[1]]],#[[1]],#[[2]]}&/@%
In[]:=
Out[]=
First/@%
In[]:=
Out[]=
Cases[%,_List]
In[]:=
Out[]=
Length/@%
In[]:=
{3,2,1,2,4,2,4,2,1,4,2,2,3,2,4,4,4,3,4,5,5,7,2,5,4,2,3,5,4,5,5,5,3,5,5,5,4,6,7,3,5,3,5,2,4,5,4,2,3,4,3,6,6,4,9,2,6,7,4,4,7,5,2,5,6,2,5,4,3,4,8,5,4,4,4,8,4,4}
Out[]=
Max[%]
In[]:=
9
Out[]=
Position[%%,9]
In[]:=
{{55}}
Out[]=
%135[[55]]
In[]:=
{2,-1,0,0,0,0,1,-2,1}
Out[]=
Cases[%133,{{2,-1,0,0,0,0,1,-2,1},_,_}]
In[]:=
{{{2,-1,0,0,0,0,1,-2,1},{2,3,4,6,8,11,14,18,22,26,31,36,42,48,55,62,69,77,85,94,103,113,123,133,144,155,167,179,192},{{1,2},{1,3}}{{1,4},{2,4},{3,4}}}}
Out[]=
ListLinePlot[Differences[{2,3,4,6,8,11,14,18,22,26,31,36,42,48,55,62,69,77,85,94,103,113,123,133,144,155,167,179,192},2]]
In[]:=
Out[]=
FindSequenceFunction[{2,3,4,6,8,11,14,18,22,26,31,36,42,48,55,62,69,77,85,94,103,113,123,133,144,155,167,179,192},t]
In[]:=
Out[]=
-1+y.[n.]-y.[1+n.]-y.[2+n.]+y.[3+n.]0
InteractiveListSelectorSW[ParallelMapMonitored[(ListLinePlot[#,TicksNone,ImageSize80]&/@Append[NestList[Differences,#[[2]],2],Ratios[#[[2]]]])#&,%133]]
In[]:=
Out[]=
Last/@{{FindLinearRecurrence[{2,3,4,5,7,9,12,16,22,29,39,51}],{2,3,4,5,7,9,12,16,22,29,39,51},{{1,2},{1,3}}{{2,4},{4,2},{3,2}}},{FindLinearRecurrence[{2,3,4,5,6,8,10,13,16,20,25,31,37,43,50,58,68,79,92,105,121,138,157,178}],{2,3,4,5,6,8,10,13,16,20,25,31,37,43,50,58,68,79,92,105,121,138,157,178},{{1,2},{1,3}}{{2,4},{4,1},{3,4}}},{FindLinearRecurrence[{2,3,4,5,7,9,11,14,18,24,30,36,44,52,60,70,82,95,108,122,138,156,175,195}],{2,3,4,5,7,9,11,14,18,24,30,36,44,52,60,70,82,95,108,122,138,156,175,195},{{1,2},{1,3}}{{2,4},{4,3},{3,1}}},{FindLinearRecurrence[{2,3,4,6,8,11,15,22,31,44,60,87,121,173}],{2,3,4,6,8,11,15,22,31,44,60,87,121,173},{{1,2},{2,3}}{{2,4},{2,1},{4,1}}},{FindLinearRecurrence[{2,3,4,5,6,8,10,11,12,14,17,21,27,34,41,49,57,65,76,93,116,144,178}],{2,3,4,5,6,8,10,11,12,14,17,21,27,34,41,49,57,65,76,93,116,144,178},{{1,2},{2,3}}{{2,4},{2,1},{3,4}}},{FindLinearRecurrence[{2,3,4,5,7,8,10,12,16,20,27,33,41,51,63,80,98,123,151,188}],{2,3,4,5,7,8,10,12,16,20,27,33,41,51,63,80,98,123,151,188},{{1,2},{2,3}}{{3,4},{3,4},{2,1}}},{FindLinearRecurrence[{2,3,4,6,7,10,12,15,19,25,31,39,50,61,73,88,107,124,148,185}],{2,3,4,6,7,10,12,15,19,25,31,39,50,61,73,88,107,124,148,185},{{1,2},{2,3}}{{4,2},{4,1},{3,2}}},{FindLinearRecurrence[{2,3,4,6,7,9,11,14,18,22,25,28,31,35,39,44,49,55}],{2,3,4,6,7,9,11,14,18,22,25,28,31,35,39,44,49,55},{{1,2},{2,3}}{{4,3},{4,1},{2,3}}}}
In[]:=
Out[]=
ParallelMapMonitored[WolframModelTest[#,Automatic,2]&,%]
In[]:=
Out[]=
#["Sizes"]&/@%
In[]:=
Out[]=
Graph[Rule@@@#["FinalState"]]&/@%%
In[]:=
Out[]=
HypergraphPlot[#,ImageSize60]&/@WolframModel[{{1,2},{1,3}}{{2,4},{4,1},{3,4}},{{0,0},{0,0}},20,"StatesList"]
In[]:=
Out[]=
AgeHypergraphPlot[WolframModel[{{1,2},{1,3}}{{2,4},{4,1},{3,4}},{{0,0},{0,0}},20],"RedBlueTones"]
In[]:=
Out[]=
AgeHypergraphPlot[WolframModel[{{1,2},{1,3}}{{2,4},{4,1},{3,4}},{{0,0},{0,0}},20],"RedBlueTones",1]
In[]:=
Out[]=
Length/@WolframModel[{{1,2},{1,3}}{{2,4},{4,1},{3,4}},{{0,0},{0,0}},50,"StatesList"]
In[]:=
{2,3,4,5,6,8,10,13,16,20,25,31,37,43,50,58,68,79,92,105,121,138,157,178,202,228,256,288,327,372,420,472,533,604,682,763,854,965,1098,1249,1414,1605,1830,2092,2386,2718,3104,3558,4082,4682,5377}
Out[]=
Length/@%
In[]:=
{2,3,4,5,6,8,10,13,16,20,25,31,37,43,50,58,68,79,92,105,121,138,157,178,202,228,256,288,327,372,420,472,533,604,682,763,854,965,1098,1249,1414,1605,1830,2092,2386,2718,3104,3558,4082,4682,5377}
Out[]=
Differences[%]
In[]:=
{1,1,1,1,2,2,3,3,4,5,6,6,6,7,8,10,11,13,13,16,17,19,21,24,26,28,32,39,45,48,52,61,71,78,81,91,111,133,151,165,191,225,262,294,332,386,454,524,600,695}
Out[]=
Differences[%]
In[]:=
{0,0,0,1,0,1,0,1,1,1,0,0,1,1,2,1,2,0,3,1,2,2,3,2,2,4,7,6,3,4,9,10,7,3,10,20,22,18,14,26,34,37,32,38,54,68,70,76,95}
Out[]=
Differences[%]
In[]:=
{0,0,1,-1,1,-1,1,0,0,-1,0,1,0,1,-1,1,-2,3,-2,1,0,1,-1,0,2,3,-1,-3,1,5,1,-3,-4,7,10,2,-4,-4,12,8,3,-5,6,16,14,2,6,19}
Out[]=
ListLinePlot[%]
In[]:=
Out[]=
WolframModel[{{x,y},{x,z}}{{x,w},{y,w},{z,w}},{{0,0},{0,0}},40,"StatesList"];
In[]:=
Length/@%
In[]:=
{2,3,4,6,8,11,14,18,22,26,31,36,42,48,55,62,69,77,85,94,103,113,123,133,144,155,167,179,192,205,218,232,246,261,276,292,308,324,341,358,376}
Out[]=
ListLinePlot[Differences[%,3]]
In[]:=
Out[]=
​
XYifyRule[{{1,2},{1,3}}{{2,4},{4,1},{3,4}}]
In[]:=
{{x,y},{x,z}}{{y,w},{w,x},{z,w}}
Out[]=
allg=Graph[Rule@@@#]&/@WolframModel[{{1,2},{1,3}}{{2,4},{4,1},{3,4}},{{0,0},{0,0}},50,"StatesList"];
In[]:=
Counts[VertexInDegree[#]]&/@allg
In[]:=
Out[]=
Counts[VertexOutDegree[#]]&/@allg
In[]:=
Out[]=
HypergraphPlot[#,ImageSize60]&/@WolframModel[{{1,2},{1,3}}{{2,4},{4,1},{3,4}},{{1,2},{1,2}},20,"StatesList"]
In[]:=
Out[]=
Graph[Rule@@@WolframModel[{{1,2},{1,3}}{{2,4},{4,1},{3,4}},{{1,2},{1,2}},20,"FinalState"],VertexLabelsAutomatic]
In[]:=
Out[]=
EdgeList[%188]
In[]:=
Out[]=
Length/@WolframModel[{{1,2},{1,3}}{{2,4},{4,1},{3,4}},{{1,2},{1,2}},50,"StatesList"]
In[]:=
{2,3,4,5,6,7,9,11,13,15,18,22,26,30,35,42,50,58,67,79,94,110,127,148,175,206,239,277,325,383,447,518,604,710,832,967,1124,1316,1544,1801,2093,2442,2862,3347,3896,4537,5306,6211,7245,8435,9845}
Out[]=
Differences[%,3]
In[]:=
{0,0,0,1,-1,0,0,1,0,-1,0,1,1,-1,-1,1,2,0,-2,0,3,2,-2,-2,3,5,0,-4,1,8,5,-4,-3,9,13,1,-7,6,22,14,-6,-1,28,36,8,-7,27,64}
Out[]=
ListLinePlot[%,MeshAll,FillingAxis,AspectRatio1/4,FrameTrue]
In[]:=
Out[]=
TentacleSize[edgelist_]:=Module[{raw,gg,len,cyc,rep,new,hh,tentacles},​​raw=Union[Sort/@(List@@@edgelist)];​​gg=Graph[UndirectedEdge@@@raw];​​len=Length[VertexList[gg]];​​cyc=First/@FindCycle[gg][[1]];​​rep=Join[cyc,Complement[Range[len],cyc]];new=Sort[Sort/@(raw/.Thread[rep->Range[Length[rep]]])];hh=Graph[UndirectedEdge@@@new];​​tentacles=Graph[Complement[EdgeList[hh],EdgeList[CycleGraph[Length[cyc]]]],VertexLabels"Name"];​​Length/@SortBy[ConnectedComponents[tentacles],Min]]
In[]:=
TentacleSize[EdgeList[UndirectedGraph[Rule@@@#]]]&/@WolframModel[{{1,2},{1,3}}{{2,4},{4,1},{3,4}},{{1,2},{1,2}},20,"StatesList"]
In[]:=
Part
:Part 1 of {} does not exist.
First
:{} has zero length and no first element.
First
:Nonatomic expression expected at position 1 in First[1].
Part
:The expression First[1] cannot be used as a part specification.
Complement
:Heads Part and List at positions 2 and 1 are expected to be the same.
Join
:Heads Part and Complement at positions 1 and 2 are expected to be the same.
Part
:Part 1 of {} does not exist.
First
:{} has zero length and no first element.
First
:Nonatomic expression expected at position 1 in First[1].
Part
:The expression First[1] cannot be used as a part specification.
Complement
:Heads Part and List at positions 2 and 1 are expected to be the same.
Join
:Heads Part and Complement at positions 1 and 2 are expected to be the same.
Part
:Part 1 of {} does not exist.
General
:Further output of Part::partw will be suppressed during this calculation.
First
:{} has zero length and no first element.
General
:Further output of First::nofirst will be suppressed during this calculation.
First
:Nonatomic expression expected at position 1 in First[1].
General
:Further output of First::normal will be suppressed during this calculation.
Part
:The expression First[1] cannot be used as a part specification.
General
:Further output of Part::pkspec1 will be suppressed during this calculation.
Complement
:Heads Part and List at positions 2 and 1 are expected to be the same.
General
:Further output of Complement::heads will be suppressed during this calculation.
Join
:Heads Part and Complement at positions 1 and 2 are expected to be the same.
General
:Further output of Join::heads will be suppressed during this calculation.
Out[]=
Take[%,-2]
In[]:=
{{6,2,2,4,3,2,4,2,6,3,2,5,3,2,2,4,2,5,3,2,3},{6,2,2,4,3,2,3,4,2,2,6,3,2,3,5,2,4,2,3,4,2,2,5,3,2,2,3}}
Out[]=
SequenceAlignment@@%
In[]:=
Out[]=