Heisenberg group
Heisenberg group
In[]:=
HeisenbergGroupCayleyGraph[mod_Integer]:=Module[{heisen3,vec,vac},heisen3=Sort[{{1,#[[1]],#[[2]]},{0,1,#[[3]]},{0,0,1}}&/@Tuples[Range[0,mod-1],{3}]];vec=Select[heisen3,Total[Flatten[#]]4&];he=Union[Sort[Flatten[Position[heisen3,#]&/@#]]&/@Flatten[Table[{#,Mod[#.vec[[v]],mod]}&/@heisen3,{v,1,3}],1]];vac=Union[Flatten[he,1]];Graph3D[UndirectedEdge@@@he,VertexCoordinatesThread[vacvec]]]
In[]:=
HeisenbergGroupCayleyGraph[mod_Integer]:=Module[{heisen3,vec,vac,heisen3edge},heisen3=Sort[{{1,#[[1]],#[[2]]},{0,1,#[[3]]},{0,0,1}}&/@Tuples[Range[0,mod-1],{3}]];vec=Select[heisen3,Total[Flatten[#]]4&];heisen3edge=Union[Sort[{#[[1,2]],#[[1,3]],#[[2,3]]}&/@#]&/@Flatten[Table[{#,Mod[#.vec[[v]],mod]}&/@heisen3,{v,1,3}],1]];vac=Union[Flatten[heisen3edge,1]];hg=Graph3D[UndirectedEdge@@@heisen3edge,VertexCoordinatesThread[vacvac]]]
In[]:=
mod=6;heisen3=Sort[{{1,#[[1]],#[[2]]},{0,1,#[[3]]},{0,0,1}}&/@Tuples[Range[0,mod-1],{3}]];vec=Select[heisen3,Total[Flatten[#]]4&];heisen3edge=Union[Sort[{#[[1,2]],#[[1,3]],#[[2,3]]}&/@#]&/@Flatten[Table[{#,Mod[#.vec[[v]],mod]}&/@heisen3,{v,1,3}],1]];vac=Union[Flatten[heisen3edge,1]];hg=Graph3D[UndirectedEdge@@@heisen3edge,VertexCoordinatesThread[vacvac]]
Out[]=
In[]:=
HeisenbergGroupCayleyGraph[3]
Out[]=
In[]:=
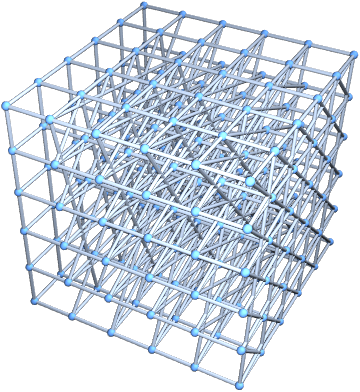
GraphNeighborhoodVolumes[#,{1}]&[HeisenbergGroupCayleyGraph[6]]
Out[]=
1{1,7,29,80,164,210,216}
In[]:=
GraphNeighborhoodVolumes[#,{1}]&[HeisenbergGroupCayleyGraph[20]]
Out[]=
1{1,7,29,83,189,379,697,1199,1953,3003,4026,4978,5740,6300,6780,7180,7500,7740,7900,7980,8000}
In[]:=
First[Values[%]]
Out[]=
{1,7,29,83,189,379,697,1199,1953,3003,4026,4978,5740,6300,6780,7180,7500,7740,7900,7980,8000}
In[]:=
Table[GraphNeighborhoodVolumes[#,{1}]&[HeisenbergGroupCayleyGraph[n]],{n,25}]
Out[]=
In[]:=
Differences[{1,7,29,83,189,379,697,1199,1953,3039},4]
Out[]=
{4,12,12,12,12,12}
In[]:=
FindSequenceFunction[{7,29,83,189,379,697,1199,1953,3039},n]
Out[]=
1
6
2
n
3
n
4
n
In[]:=
%204/.nn-1
Out[]=
1
6
2
(-1+n)
3
(-1+n)
4
(-1+n)
In[]:=
Expand[%]
Out[]=
39-+-+
145n
3
43
2
n
2
11
3
n
3
4
n
2
In[]:=
Table[%,{n,10}]
Out[]=
{9,7,29,83,189,379,697,1199,1953,3039}
In[]:=
First/@Values[Rest[%198]]
Out[]=
In[]:=
ListLogLogPlot[%]
Out[]=