Bundle of geodesics
Bundle of geodesics
Optimization
Optimization
mm=;
In[]:=
MinSumPermutation[mm_?MatrixQ]:=Module[{n,m,objective,constraints,vars,res,p},{n,m}=Dimensions[mm];objective=Total[Inactive[Times][p,mm],2];constraints={Table[Sum[Indexed[p,{i,j}],{j,m}]1,{i,n}],Table[Sum[Indexed[p,{i,j}],{i,n}]≤1,{j,m}],0p1};vars={Element[p,Matrices[{n,m},Integers]]};res=LinearOptimization[objective,constraints,vars];Flatten[SparseArray[p/.res]["NonzeroPositions"][[All,2]]]]
In[]:=
With[{perm=Echo[MinSumPermutation[mm]]},Sum[mm[[i,perm[[i]]]],{i,Length[mm]}]]
In[]:=
{6,12,5,9,2,3,13,10,16,4,7,1,19,8,17,14,18,15,11}
»
701
Out[]=
GeodesicsBundle
GeodesicsBundle
GeodesicsBundle[graph_,endpoints:{_Integer,_Integer},neighborhoodSize_:3,plottingFunction_:GeodesicsAll]:=Module[{neighborhoods,distanceMatrix,matchingEndpoints},neighborhoods=VertexList[NeighborhoodGraph[graph,#,neighborhoodSize]]&/@endpoints;distanceMatrix=Outer[GraphDistance[graph,#1,#2]&,neighborhoods〚1〛,neighborhoods〚2〛];matchingEndpoints=If[Dimensions[distanceMatrix]〚1〛≥Dimensions[distanceMatrix]〚2〛,Transpose[{neighborhoods〚1,MinSumPermutation[Transpose@distanceMatrix]〛,neighborhoods〚2〛}],Transpose[{neighborhoods〚1〛,neighborhoods〚2,MinSumPermutation[distanceMatrix]〛}]];plottingFunction[graph,matchingEndpoints]]
In[]:=
GeodesicsBundle[graph_,endpointFractions:{_Real,_Real},neighborhoodSize_:3]:=Module[{path,endpoints},path=FindShortestPath[graph,Sequence@@GraphAntipodes[graph]];endpoints=path〚Round[endpointFractionsLength[path]]〛;GeodesicsBundle[graph,endpoints,neighborhoodSize]]
In[]:=
GeodesicsBundle[graph_,neighborhoodSize_:3]:=GeodesicsBundle[graph,{0.2,0.8},neighborhoodSize]
In[]:=
GeodesicsAll
GeodesicsAll
ShortestPathsVertices[graph_,v1_,v2_]:=VertexList[graph]〚Position[MapThread[Plus,{GraphDistance[graph,v1],GraphDistance[graph,v2]}],GraphDistance[graph,v1,v2]]〚All,1〛〛
In[]:=
GeodesicsAll[g_Graph,vpairs:{{_,_}..}]:=HighlightGraph[g,Style[Subgraph[g,Catenate[ShortestPathsVertices[g,##]&@@@vpairs]],Thickness[.02],Red]]
In[]:=
Buckyball
Buckyball
Row[Show[GeodesicsBundle[BuckyballGraph[7,"Embedded"],#],ImageSize300]&/@Range[3,6]]
In[]:=
Out[]=
With[{ball20=BuckyballGraph[20,"Embedded"]},Row[Show[GeodesicsBundle[ball20,#],ImageSize300]&/@Range[3,6]]]
In[]:=
$Aborted
Out[]=
Hexagonal graph
Hexagonal graph
HexagonalGrid[width_?EvenQ, height_?EvenQ] := SimpleGraph @ GraphCatenate @ CatenateThread /@ TableIfEvenQ[i + Ceiling[i / width]], Int[i] If[i - width ≥ 1, Int[i - width], Ext[i]], If[i + width ≤ width height, Int[i + width], Ext[Mod[i - 1, width] + 1 + width]], IfMod[i, width] 0, Ext, Int[i + 1] , Int[i] If[i - width ≥ 1, Int[i - width], Ext[i]], IfMod[i, width] 1, Ext, Int[i - 1], If[i + width ≤ width height, Int[i + width], Ext[Mod[i - 1, width] + 1 + width]] , {i, 1, width height} /. Missing[] Ext[RandomInteger[{0, -1}]], Table Ifi ≤ width, Ext[i] Int[i], Ifi ≤ 2 width, Ext[i] Int[width (height - 2) + i], Ifi ≤ 2 width + , Ext[i] Int[(i - 2 width) 2 width - width + 1], Ext[i] Inti - 2 width - 2 width , {i, 1, 2 width + height}, DirectedEdges False
Quotient[i, width] + 4 width + height
2
Quotient[i, width] + 4 width + 1
2
64
2
height
2
height
2
In[]:=
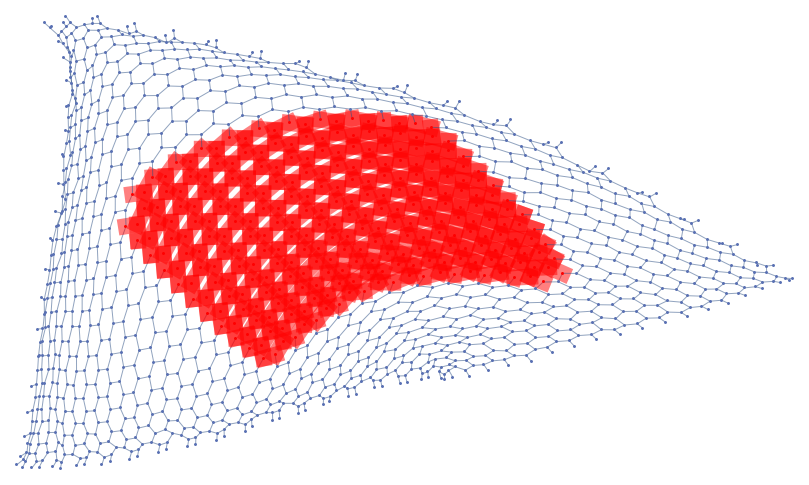
GeodesicsBundle[IndexGraph[HexagonalGrid[36,36]],{713,730},3]
In[]:=
Out[]=
Similar effect seems to be happening to the spheres.
Discretized sphere
Discretized sphere
GeodesicsBundle[IndexGraph@MeshConnectivityGraph[DiscretizeGraphics[Sphere[]]],1]
In[]:=
Out[]=
GeodesicsBundle[IndexGraph@MeshConnectivityGraph[DiscretizeGraphics[Sphere[],MaxCellMeasure0.0001]],1]
In[]:=
Out[]=
SpherePoints
SpherePoints
GraphPlot3D[GeodesicsBundle[IndexGraph[NearestNeighborGraph[SpherePoints[1000],4]],1]]
In[]:=
Out[]=
GraphPlot3D[GeodesicsBundle[IndexGraph[NearestNeighborGraph[SpherePoints[10000],4]],1]]
In[]:=
Out[]=
Random points
Random points
GraphPlot3D[GeodesicsBundle[IndexGraph[NearestNeighborGraph[RandomPoint[Sphere[],1000],4]],2]]
In[]:=
Out[]=
GraphPlot3D[GeodesicsBundle[IndexGraph[NearestNeighborGraph[RandomPoint[Sphere[],10000],4]],{0.3,0.7}]]
In[]:=
Out[]=
GraphPlot3D[GeodesicsBundle[IndexGraph[NearestNeighborGraph[RandomPoint[Sphere[],10000],4]],{0.3,0.7},5]]
In[]:=
Out[]=
GraphPlot3D[GeodesicsBundle[IndexGraph[NearestNeighborGraph[RandomPoint[Sphere[],10000],10]],{0.3,0.7},3]]
In[]:=
Out[]=
Maybe measure how they diverge statistically?
GraphPlot3D[GeodesicsBundle[IndexGraph[NearestNeighborGraph[RandomPoint[Sphere[],10000],4]],{0.1,0.9},3]]
In[]:=
Out[]=
GraphPlot3D[GeodesicsBundle[IndexGraph[NearestNeighborGraph[RandomPoint[Sphere[],10000],4]],{0.1,0.9},3]]
In[]:=
Out[]=
Partial conclusion
Partial conclusion
We are getting discretization effects: either due to (non-isotropic) grid, or due to randomness.
We need to get away from these effects by making the graphs large: the graph itself should be large ( vertices), the geodesics should be long (~1000 vertices), the bundle radius should be large (). In that case, we should be able to get results that start to approximate continuous case, however, we won’t be able to see the grid at that scale.
~
6
10
~100
Mesh Ellipsoid
Mesh Ellipsoid
Ellipsoid diverge one direction vs. the other direction
Ellipsoid diverge one direction vs. the other direction
Cylinder growth going one or another way around the ellipsoid
Cylinder growth going one or another way around the ellipsoid
Network for deSitter or anti-deSitter space
Network for deSitter or anti-deSitter space