You are using a browser not supported by the Wolfram Cloud
Supported browsers include recent versions of Chrome, Edge, Firefox and Safari.
I understand and wish to continue anyway »
WOLFRAM NOTEBOOK
gtest=UndirectedGraph[Rule@@@WolframModel[{{x,y},{x,z}}{{x,z},{x,w},{y,w},{z,w}},{{1,2},{1,3}},10,"FinalState"]]
In[]:=
GeodesicBundle[g_Graph,{v1_,v2_},r_]:=Module[{spf=FindShortestPath[g,All,All],n1=NeighborhoodGraph[g,v1,r],n2=NeighborhoodGraph[g,v2,r]},HighlightGraph[g,Style[#,Thick,Red]&/@Flatten[Outer[PathGraph[spf[#1,#2]]&,VertexList[n1],VertexList[n2]]]]]
In[]:=
GeodesicBundle[g_Graph,{v1_,v2_},0]:=Module[{spf=FindShortestPath[g,All,All],n1=Graph[{v1},{}],n2=Graph[{v2},{}]},HighlightGraph[g,Style[#,Thick,Red]&/@Flatten[Outer[PathGraph[spf[#1,#2]]&,VertexList[n1],VertexList[n2]]]]]
In[]:=
Geodesics[g_Graph,vpairs:{{_,_}..}]:=HighlightGraph[g,Style[PathGraph[FindShortestPath[g,#[[1]],#[[2]]]],Thickness[.02],Red]&/@vpairs]
In[]:=
GeodesicsAll[g_Graph,vpairs:{{_,_}..}]:=HighlightGraph[g,ParallelMapMonitored[(Style[PathGraph[#],Thick,Red]&/@FindPath[g,#[[1]],#[[2]],{GraphDistance[g,#[[1]],#[[2]]]},All])&,vpairs]]
RandomGeodesic[gx_,n_Integer:1]:=With[{g=IndexGraph[gx,EdgeStyleLightGray,VertexStyleLightGray]},With[{spf=FindShortestPath[g,All,All],vl=VertexList[g]},HighlightGraph[g,Table[Style[PathGraph[spf[RandomChoice[vl],RandomChoice[vl]]],Thick,RandomColor[]],n]]]]
In[]:=
sph=IndexGraph@MeshConnectivityGraph[DiscretizeGraphics[Sphere[]]]
Out[]=
In[]:=
VertexList[sph]
In[]:=
GeodesicBundle[sph,{1,600},1]
Out[]=
In[]:=
GeodesicBundle[sph,{1,600},0]
Out[]=
In[]:=
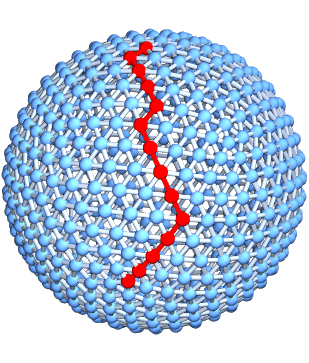
Geodesics[sph,{{1,600}}]
Out[]=
In[]:=
GeodesicsAll[sph,{{1,600}}]
Out[]=
In[]:=
GeodesicsAll[sph,{{1,600},{86,182}}]
Out[]=
$Aborted
In[]:=
NeighborhoodGraph[sph,1,VertexLabelsAutomatic]
Out[]=
WM geodesic
WM geodesic
Examples
Examples