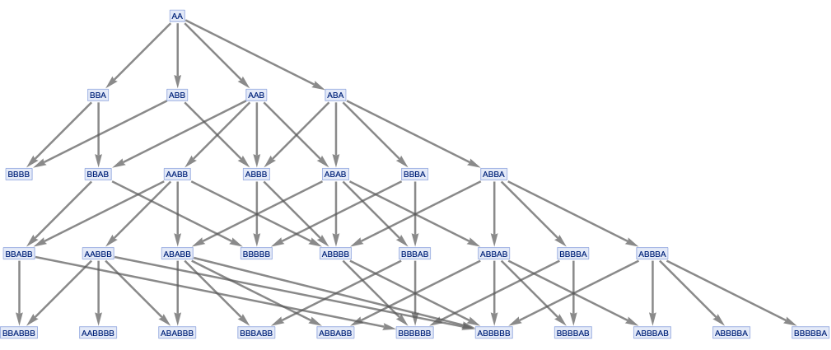
In[]:=
gmw=GenerationalMultiwaySystem[{"A""AB","A""BB"},{"AA"},4,"StatesGraph"]
Out[]=
In[]:=
mw=MultiwaySystem[{"A""AB","A""BB"},{"AA"},4,"StatesGraph"]
Out[]=
Two different ways to get a generational state:
1. Snaking together individual update results at a given ordinary multiway depth
2. Wait until the generational state is formed through individual updates
1. Snaking together individual update results at a given ordinary multiway depth
2. Wait until the generational state is formed through individual updates
Eventually the full generational state will be assembled ... but it may take a while
Alternative: be a more sophisticated observer, and aggregate the eigenstates to come up with a “classical” interpretation of a given superposition
Alternative: be a more sophisticated observer, and aggregate the eigenstates to come up with a “classical” interpretation of a given superposition
In the mind of the observer, the individual string fragments are being assembled into a “generational” string.
[ Causal invariance as emergent because of additional “non-physics” updates/equivalences ] [ physics + the mind => classical interpretation ]
Relation of causal invariance to foliatability of the multiway graph
Relation of causal invariance to foliatability of the multiway graph
Natural occurring causal invariance: i.e. it is immediately causal invariance
Completability: finite number of equivalences can get you causal invariance
Completability: finite number of equivalences can get you causal invariance
There is still a spacelike story for strings ..... different updates are happening in different places
There is still a spacelike story for strings ..... different updates are happening in different places
Even the strings have a light cone
General spacelike separation:
General spacelike separation:
Each individual “state” (aka string from individual updates) is a full state of the system ... but .....
Each individual “state” (aka string from individual updates) is a full state of the system ... but .....
It is causally consistent to assemble it into a generational state because of spacelike separation......
Generationalization is beyond foliation
Generationalization is beyond foliation
Different foliation of underlying multiway graph could lead (in the case of some non-spacelike separated events) to a different generational multiway graph
Generationalization uses spacelike “independence”
Generationalization uses spacelike “independence”
Generationalization vs. foliation:
Generationalization vs. foliation:
Given a foliation, you can aggregrate states within that foliation into generational states
Multiway causal graph:
Multiway causal graph:
In the GMW graph, every arrow is a bundle of spacelike separated events