Involutions[n_]:=(I/Sqrt[2])^nHermiteH[n,-I/Sqrt[2]];
In[]:=
Involutions[n_]:=Sum[StirlingS1[n,k]*2^k*BellB[k,1/2],{k,0,n}]
In[]:=
Involutions[4]
Out[]=
10
In[]:=
Array[Involutions,20]
Out[]=
{1,2,4,10,26,76,232,764,2620,9496,35696,140152,568504,2390480,10349536,46206736,211799312,997313824,4809701440,23758664096}
self-inverse permutations
All total orderings
All total orderings
In[]:=
IntegerPartitions[6]
Out[]=
{{6},{5,1},{4,2},{4,1,1},{3,3},{3,2,1},{3,1,1,1},{2,2,2},{2,2,1,1},{2,1,1,1,1},{1,1,1,1,1,1}}
In[]:=
youngall=Catenate[Tableaux/@IntegerPartitions[6]]
Out[]=
In[]:=
Length[young]
Out[]=
76
In[]:=
Divisors[76]
Out[]=
{1,2,4,19,38,76}
In[]:=
skewall=SkewPoset/@YoungTableauToPoset/@Catenate[Tableaux/@IntegerPartitions[6]];
In[]:=
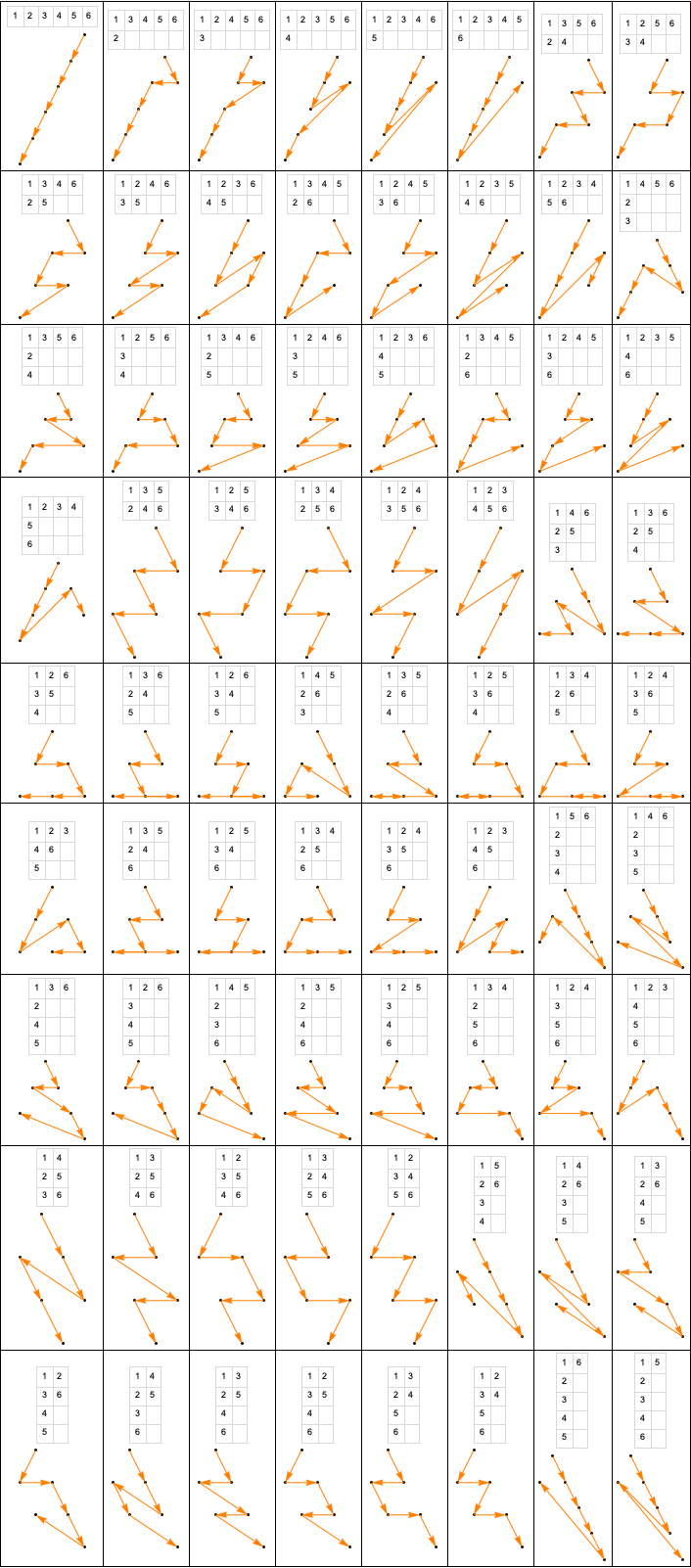
SkewPosetDiagram[#,ImageSize30]&/@skewall
Out[]=
In[]:=
Grid[Partition[Column[#,AlignmentCenter]&/@Transpose[{Grid[Map[Text[Style[#,Small]]&,#,{2}],FrameAll,FrameStyleLightGray]&/@young,SkewPosetDiagram[#,ImageSize70]&/@skew}],8],FrameAll]
Out[]=
In[]:=
n
2
∑
k=0
n |
2k |
Out[]=
1-n
1
2
2
1-n
2
3
2
1
2
In[]:=
Series[%63,{n,Infinity,2}]
Out[]=
-+n+-+
π
2
Log[2]
2
π
2
Log[2]
2
3
O
1
n
1
2
n
2
3
2
1
2
In[]:=
DiscreteAsymptotic[%,nInfinity]
Out[]=
π
2
π
2
Log[2]
2
1
2
n
2
3
2
1
2
2
In[]:=
Involutions[n_]:=Sum[(2k-1)!!Binomial[n,2k],{k,0,n/2}];
In[]:=
as[n_]:=Exp[Sqrt[n]-n/2-1/4]n^(n/2)/Sqrt[2]
In[]:=
RecurrenceTable[{(-1-n)a[n]-a[1+n]+a[2+n]0,a[1]1,a[2]2},a,{n,200}]
Out[]=